At what distance from a convex lens of focal length 30cm an object should be placed so that the size of image be 14that of object?
30 cm
60 cm
15 cm
150 cm
The correct Answer is:D
To solve the problem, we need to determine the distance at which an object should be placed from a convex lens so that the size of the image is one-fourth that of the object.
1. Identify Given Values:
- Focal length of the convex lens, f=+30cm (positive because it's a convex lens).
- Size of the image is one-fourth that of the object, which implies the magnification m=h′h=14.
2. Determine the Type of Image:
- Since the image size is smaller than the object, the image is real and inverted. Therefore, the magnification is given by:
m=−vu
- Here, v is the image distance and u is the object distance.
3. Express Image Distance in Terms of Object Distance:
- From the magnification formula, we have:
−vu=14
- Rearranging gives:
v=−14u
4. Use the Lens Formula:
- The lens formula is given by:
1f=1v−1u
- Substituting f=30cm and v=−14u:
130=1−14u−1u
5. Simplify the Equation:
- The term 1−14u simplifies to −4u:
130=−4u−1u
- Combine the terms on the right:
130=−5u
6. Solve for u:
- Rearranging gives:
5u=−130
- Cross-multiplying results in:
5⋅30=−u
- Thus:
u=−150cm
7. Determine the Object Distance:
- Since u is negative, it indicates that the object is placed 150 cm in front of the lens.
Final Answer:
The object should be placed at a distance of 150 cm from the convex lens.
---
- Focal length of the convex lens, f=+30cm (positive because it's a convex lens).
- Size of the image is one-fourth that of the object, which implies the magnification m=h′h=14.
- Since the image size is smaller than the object, the image is real and inverted. Therefore, the magnification is given by:
m=−vu
- Here, v is the image distance and u is the object distance.
- From the magnification formula, we have:
−vu=14
- Rearranging gives:
v=−14u
- The lens formula is given by:
1f=1v−1u
- Substituting f=30cm and v=−14u:
130=1−14u−1u
- The term 1−14u simplifies to −4u:
130=−4u−1u
- Combine the terms on the right:
130=−5u
- Rearranging gives:
5u=−130
- Cross-multiplying results in:
5⋅30=−u
- Thus:
u=−150cm
- Since u is negative, it indicates that the object is placed 150 cm in front of the lens.
The object should be placed at a distance of 150 cm from the convex lens.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.5
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.6
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.3
20 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
A ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. The emergent ray of light makes an angle fo 30∘ with incident ray. Tha angle made by the emergent ray with second face of prism will be :
View SolutionThe least distance of distinct vision for a young adult with normal vision is about
View SolutionA light wave has a frequency of 4×1014Hz and a wavelength of 5×10−7 meters in a medium. The refractive index of the medium is
View SolutionThe half-life of a radioactive substance is 30 minutes, The time (in minutes) taken between 40% decay and 85% decay of the same radioactive substance is.
View SolutionA point source of light S is placed at a distance 10 cm in front of the centre of a mirror of width 20 cm suspended vertically on a wall. An insect walks with a speed 10cm/s in front of the mirror along a line parallel to the mirror at a distance 20 cm from it as shown in figure. find the maximum time during which the insect can see the image of the source S in the mirror.
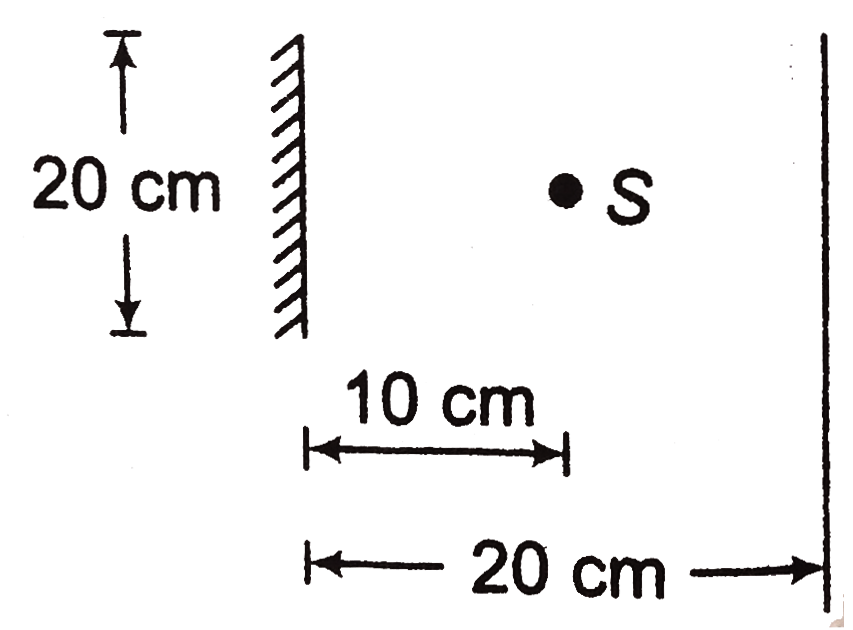
View SolutionFind the position, nature and size of the image formed by a convex lens of focal length 20 cm of an object 4 cm high placed at a distance of 30cm from it.
View SolutionA convex lens of focal length f produces a virtual image n times the size of the object. Then the distance of the object from the lens is
View SolutionAt what distance from a convex lens of focal length 30cm an object should be placed so that the size of image be (1)/(4) that of object?
View SolutionThe focal length of a convex lens is 30cm and the size of the real image is 14th of the object. Then the object distance is
View SolutionA convex lens forms a real and inverted image of a pencil at a distance of 40 cm from the lens. The image formed is of the same size as the object Find the focal length and power of the lens. At what distance is the : object placed from the lens?
View SolutionA concave lens of focal length f produces an image (1)/(4) of the size of the object, the object should be kept at ____ from the lens.
View SolutionA point object is placed at a distance of 30cm from a convex mirror of focal length 30cm. The image will from at
View Solutionएक उत्तल लेन्स की फोकस दूरी f है जो कि वस्तु के आकार का 1n गुना प्रतिबिम्ब बनाता है । वस्तु की लेन्स से दूरी होगी
View SolutionA convex lens of focal length f produces a real image m times the size of an object, then the distance of the object from the lens is
View SolutionImage of an object at infinity is formed by a convex lens of focal length 30cm such that the size of the image is 2cm. If a concave lens of focal length 20cm is placed in between the convex lens and the image, at a distance 26cm from the convex lens, size of the new image is
View Solution
