Two lenses have focal lengths f1 and f2 and their dispersive powers are ω1 and ω2 respectively. They will together form an achromatic combination if
ω1f1=ω2f2
ω1f2+ω2f1=0
ω1+f1=ω2+f2
ω1−f1=ω2−f2
The correct Answer is:B
To determine the condition for two lenses to form an achromatic combination, we can follow these steps:
1. Understanding the Concept:
- An achromatic combination of lenses is one where the combination does not disperse light into its constituent colors. This is achieved when the chromatic aberration introduced by the two lenses cancels each other out.
2. Using the Formula:
- The condition for two lenses to form an achromatic combination can be expressed mathematically. The formula is:
ω1f1+ω2f2=0
where ω1 and ω2 are the dispersive powers of the two lenses, and f1 and f2 are their respective focal lengths.
3. Cross-Multiplying:
- Rearranging the formula gives:
ω1f2+ω2f1=0
This indicates that the sum of the products of the dispersive power and focal lengths must equal zero.
4. Identifying the Correct Option:
- Now, we will check the provided options against our derived equation:
- Option 1: ω1f1=ω2f2 (not correct)
- Option 2: ω1f2+ω2f1=0 (correct)
- Option 3: ω1+f1=ω2+f2 (not correct)
- Option 4: ω1−f1=ω2−f2 (not correct)
5. Conclusion:
- The correct condition for the two lenses to form an achromatic combination is given by:
ω1f2+ω2f1=0
Therefore, the answer is Option 2.
- An achromatic combination of lenses is one where the combination does not disperse light into its constituent colors. This is achieved when the chromatic aberration introduced by the two lenses cancels each other out.
- The condition for two lenses to form an achromatic combination can be expressed mathematically. The formula is:
ω1f1+ω2f2=0
where ω1 and ω2 are the dispersive powers of the two lenses, and f1 and f2 are their respective focal lengths.
- Rearranging the formula gives:
ω1f2+ω2f1=0
This indicates that the sum of the products of the dispersive power and focal lengths must equal zero.
- Now, we will check the provided options against our derived equation:
- Option 1: ω1f1=ω2f2 (not correct)
- Option 2: ω1f2+ω2f1=0 (correct)
- Option 3: ω1+f1=ω2+f2 (not correct)
- Option 4: ω1−f1=ω2−f2 (not correct)
- The correct condition for the two lenses to form an achromatic combination is given by:
ω1f2+ω2f1=0
Therefore, the answer is Option 2.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Exercise
170 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.6
20 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
Focal length of two lens arefandf′and dispersive powers are ω0and 2ω0.To form achromatic combination from these-
(1)f′=2f,(2)f′=−2f (3)f′=−f/2
View SolutionTwo thin lenses of focal length f1 and f2 are in contact and coaxial. The power of the combination is
View SolutionTwo thin lenses of focal lengths f1 and f2 are in contact. The focal length of this combination is
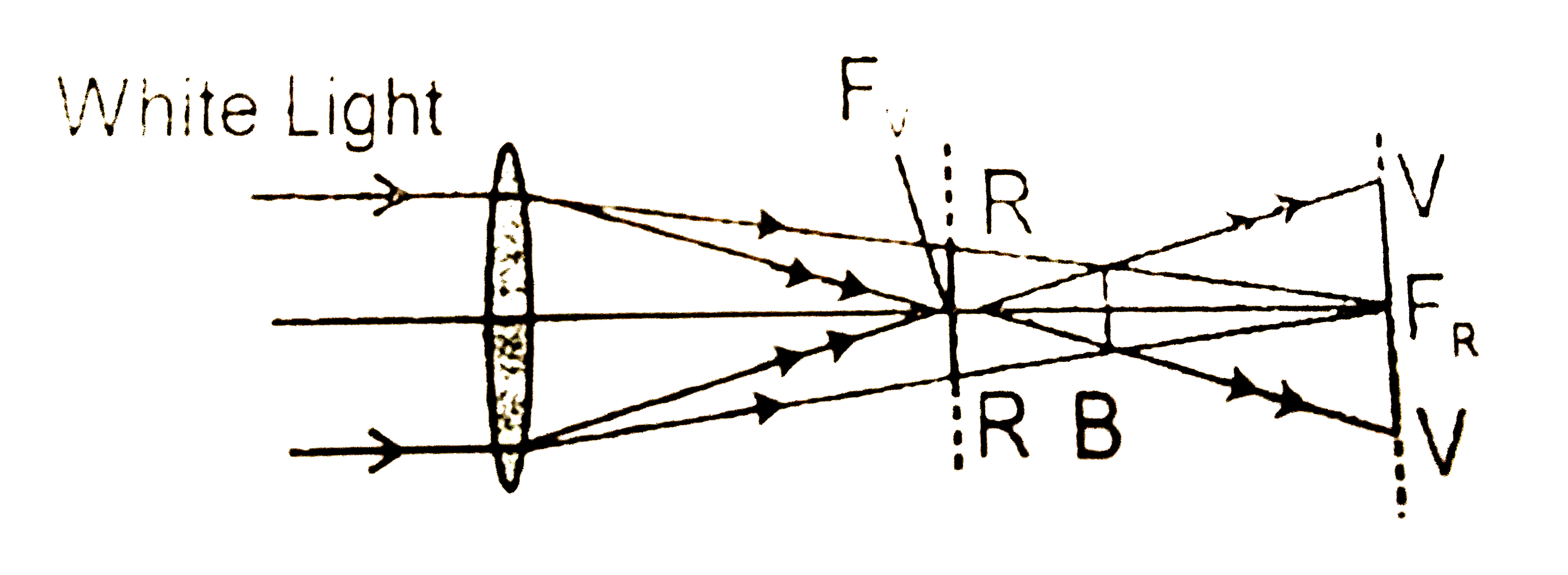
View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
A combination is made of two lenses of focal lengths f and f' in contact , the dispersive powers of the materials of the lenses are ω and ω' . The combination is achromatic when :
View SolutionAn achromatic doublet is formed by combining two lenses.if the focal length of the lenses and their dispersive powers are f,f′and ω,ω′ respectively then
View SolutionIt is desired to make an achromatic combination of two lenses, (L1&L2) made of materials having dispersive power ω1 and ω2(<ω1). If the combination of lenses is converging then:
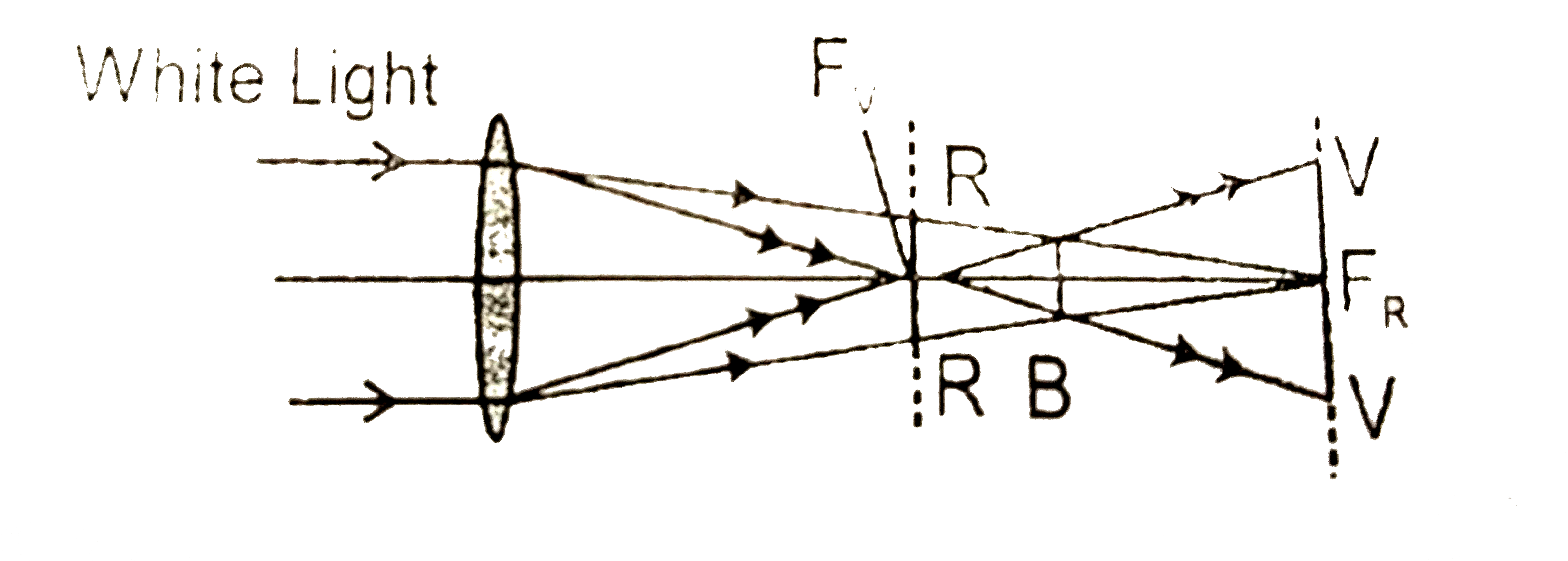
View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
The dispersive power of crown and fint glasses are 0.02 and 0.04 respectively. An achromtic converging lens of focal length 40cm is made by keeping two lenses, one of crown glass and the other of flint glass, in contact with each other. The focal lengths of the two lenses are :
View SolutionIn the figure shown, there are two convex lenses L1 and L2 having focal. Lengths f1 and f2 respectively. The distance between L1 and L2 will be
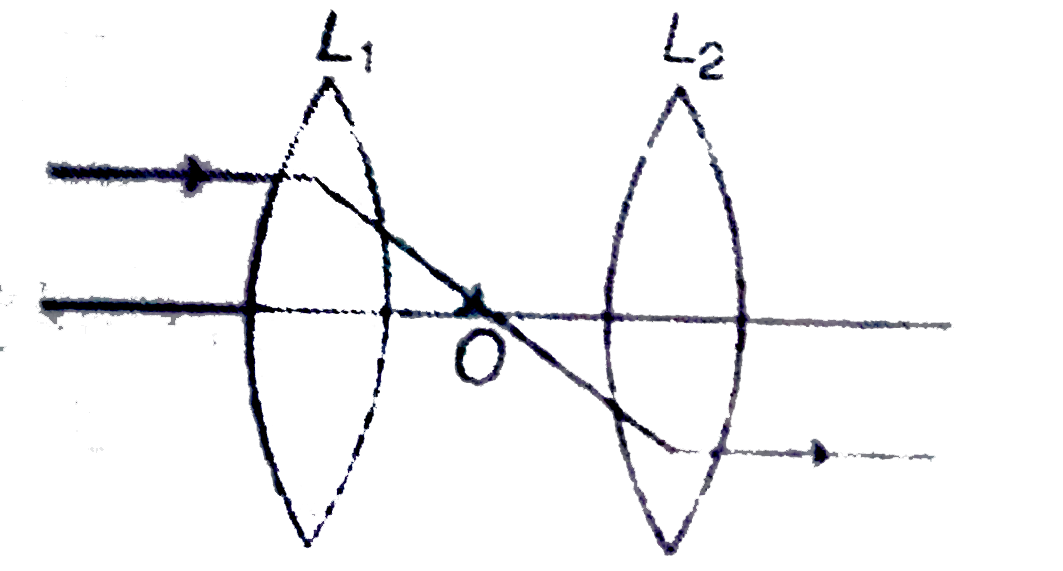
View SolutionTwo converging lenses have focal length f1andf2 The optical axes of the two lenses coincide. This lens system is used to form an image of an object . It is observed that the size of the image does not depend on the distance between the system and object . The distance between lenses is
View SolutionA plano-convex lens (focal length f2, refractive indexμ2, radius of curvature R) fits exactly into a plano-concave lens (focal lengthf1 refractive index μ1, radius of curvature R). Their plane surfaces are parallel to each other. Then, the focal length of the combination will be :
View Solution
