A mark at the bottom of a liquid appears to rise by 0.1m. The depth of the liquid is 1m. The refractive index of the liquid is
1.33
43718
109
1.5
The correct Answer is:C
To find the refractive index of the liquid based on the information provided, we can follow these steps:
Step 1: Understand the problem
We have a mark at the bottom of a liquid that appears to rise by 0.1 m. The actual depth of the liquid is 1 m. We need to find the refractive index of the liquid.
Step 2: Identify the real and apparent depths
- Real Depth (d): This is the actual depth of the liquid, which is given as 1 m.
- Apparent Depth (d'): Since the mark appears to rise by 0.1 m, the apparent depth can be calculated as:
d′=d−0.1m=1m−0.1m=0.9m
Step 3: Use the formula for refractive index
The refractive index (μ) of the liquid can be calculated using the formula:
μ=Real DepthApparent Depth=dd′
Substituting the values we have:
μ=1m0.9m=109
Step 4: Conclusion
Thus, the refractive index of the liquid is:
μ=109
We have a mark at the bottom of a liquid that appears to rise by 0.1 m. The actual depth of the liquid is 1 m. We need to find the refractive index of the liquid.
- Real Depth (d): This is the actual depth of the liquid, which is given as 1 m.
- Apparent Depth (d'): Since the mark appears to rise by 0.1 m, the apparent depth can be calculated as:
d′=d−0.1m=1m−0.1m=0.9m
The refractive index (μ) of the liquid can be calculated using the formula:
μ=Real DepthApparent Depth=dd′
Substituting the values we have:
μ=1m0.9m=109
Thus, the refractive index of the liquid is:
μ=109
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question23videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary76videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.710videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY46videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
Similar Questions
The pressure at the bottom of a liquid container is determined by the
View SolutionThe apparent depth of a liquid in a vessel is 15 cm, when its real depth is 20 cm. find the refractive index of the liquid.
View SolutionYoung's double slit experiment is made in a liquid. The tenth bright fringe in liquid lies in screen where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
View SolutionYoung's double slit experiment is made in a liquid. The tenth bright fringe in liquid lies in screen where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
View SolutionA coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View SolutionA point source S is placed at the bottom of a transparent block of height 10mm and refractive index 2.72. It is immersed in a lower refractive index liquid as shwon in Fig. I tis found that the light emerging from the block to the liquid forms a circular bright spot of diameter 11.54mm on the top of the block. The refractive index of the liquid is
 View Solution
View SolutionA vesserl contains a slab of glass 8cm thick and of refractive index 1.6 . Over the slab, the vessel is filled by oil of refractive index μ upto height 4.5 cm and then by another liquid, i.e., water of refractive index 4/3 and height 6cm as shown in Figure. An observer looking down from above observer that a mark at the bottom of glass slab appears to be raised up to a position 6cm from bottom of the slab. Find refractive index of oil (μ) .
 View Solution
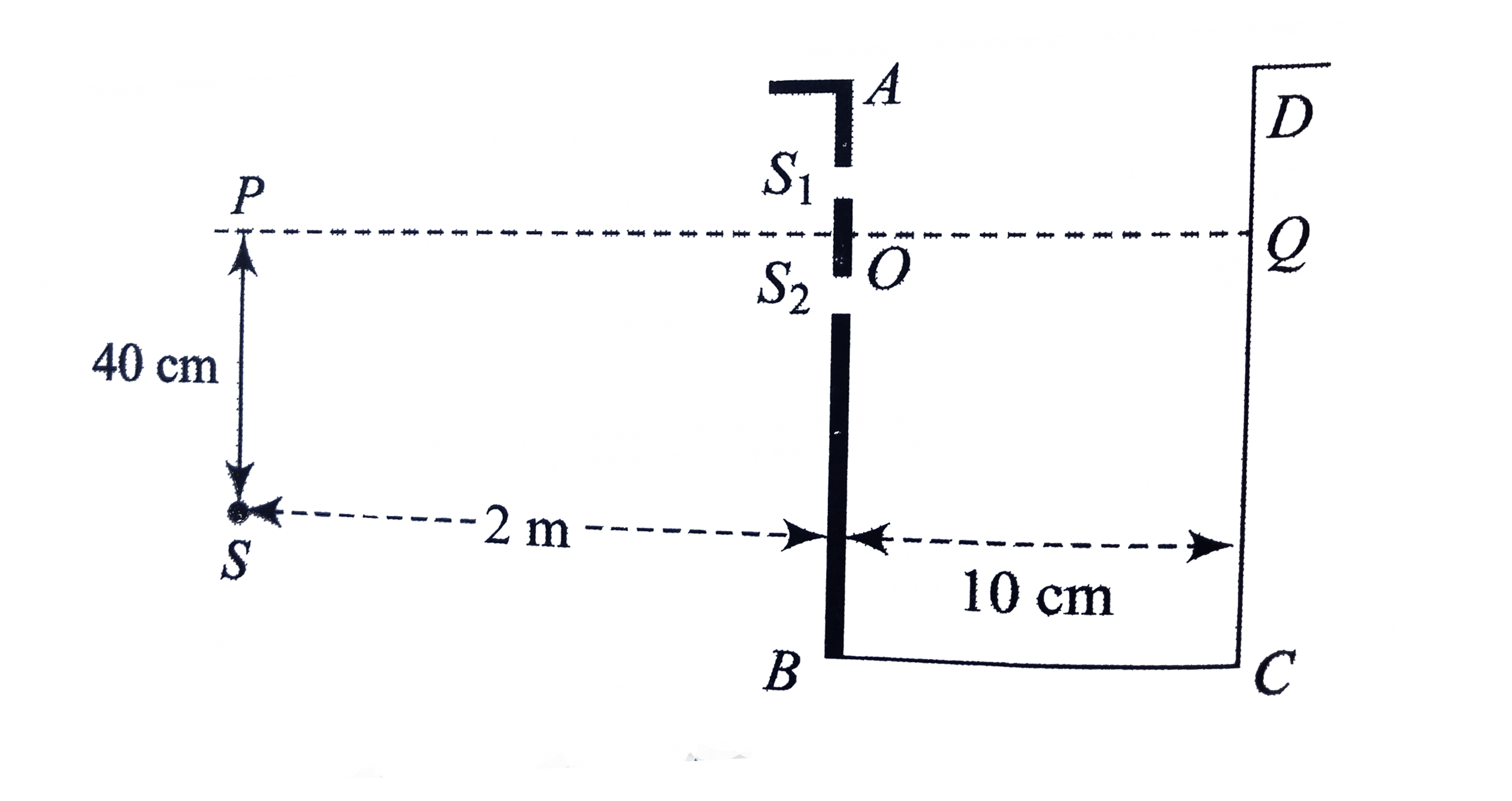
View SolutionA vessel ABCD of 10 cm width has two small slits S1 and S2 sealed with identical glass plates of equal thickness. The distance between the slits is 0.8 mm. POQ is the line peropendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S, 40 cm below P and 2 m form the vessel to illuminate the slits as shown in figure .Calculate the position of the central bright fringe on the other wall CD with respect to line OQ. Now , a liquid is poured into the vessel and filled up to OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid to the liquid.
 View Solution
View SolutionA bird in air looks at a fish directly below it inside in a transparent liquid in a tank. If the distance of the fish as estimated by the bird is h1 and that of the bird as estimated by the fish is h2, then the refractive index of the liquid is
View SolutionA convex lens is held 45cm above the bottom of an empty tank. The image of a point at the bottom of a tank is formed 36cm above the lens. Now, a liquid is poured into the tank to a depth of 40cm. It is found that the distance of the image of the same point on the bottom of the tank is 48cm above the lens. Find the refractive index of the liquid.
View Solution

