Young's double slit experiment is made in a liquid. The tenth bright fringe in liquid lies in screen where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
1.8
1.54
1.67
1.2
The correct Answer is:A
To solve the problem regarding Young's double slit experiment in a liquid, we need to analyze the relationship between the bright and dark fringes in both the liquid and vacuum. Here's a step-by-step solution:
Step 1: Understand the fringe conditions
In Young's double slit experiment, the position of bright and dark fringes is given by the formulas:
- Bright fringe: yn=nλDd
- Dark fringe: ym=(m+12)λDd
Where:
- n is the order of the bright fringe
- m is the order of the dark fringe
- λ is the wavelength of light in vacuum
- D is the distance from the slits to the screen
- d is the distance between the slits
Step 2: Relate the fringes in liquid and vacuum
Given that the 10th bright fringe in the liquid coincides with the 6th dark fringe in vacuum, we can set up the equations for both conditions.
For the 10th bright fringe in liquid:
y10=10λ′dD
Where λ′=λμ (the wavelength in the liquid).
For the 6th dark fringe in vacuum:
y6=(6+12)λdD=132λdD
Step 3: Equate the two positions
Since both positions correspond to the same point on the screen:
10λ′dD=132λdD
Step 4: Simplify the equation
Cancel D and d from both sides:
10λ′=132λ
Substituting λ′=λμ:
10(λμ)=132λ
Step 5: Solve for the refractive index μ
Now, we can solve for μ:
101μ=132
μ=10×213=2013
Step 6: Approximate the refractive index
Calculating 2013:
μ≈1.54
Final Answer
The refractive index of the liquid is approximately μ≈1.54.
---
In Young's double slit experiment, the position of bright and dark fringes is given by the formulas:
- Bright fringe: yn=nλDd
- Dark fringe: ym=(m+12)λDd
- n is the order of the bright fringe
- m is the order of the dark fringe
- λ is the wavelength of light in vacuum
- D is the distance from the slits to the screen
- d is the distance between the slits
Given that the 10th bright fringe in the liquid coincides with the 6th dark fringe in vacuum, we can set up the equations for both conditions.
y10=10λ′dD
Where λ′=λμ (the wavelength in the liquid).
y6=(6+12)λdD=132λdD
Since both positions correspond to the same point on the screen:
10λ′dD=132λdD
Cancel D and d from both sides:
10λ′=132λ
Substituting λ′=λμ:
10(λμ)=132λ
Now, we can solve for μ:
101μ=132
μ=10×213=2013
Calculating 2013:
μ≈1.54
The refractive index of the liquid is approximately μ≈1.54.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Objective question
2 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1Subjective
22 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason
10 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
Young's double slit experiment is first performed in air and then in a medium other than air. It is found than 8th bright fringe in the medium lies where 5th daek fringe lies in air. The re3fractive index of the medium is nearly
View SolutionAssertion:- When a width of one of the slits of Young's double slit experiment is double that of the other the brighter frings are nine times brighter then the dark fringes.
Reason:- The amplitudes of the wave is proportional to the width of the slit.
View Solution
Knowledge Check
A Young's double slit experiment uses a monochromatic source. The shape of the interference fringes formed on a screen is
AparabolaBstraight lineCcircleDhyperbola
In young's double slit experiment, fringe order is represented by m, then fringe width is
View SolutionIn Young's double slit experiment, the phase difference between the two waves reaching at the location of the third dark fringe is
View SolutionIn the Young’s double slit experiment, for which colour the fringe width is least
View SolutionWhen entire Young's double slit apparatus is immersed in a liquid the fringe width decreases by 20∘. The refractive index of the liquid is
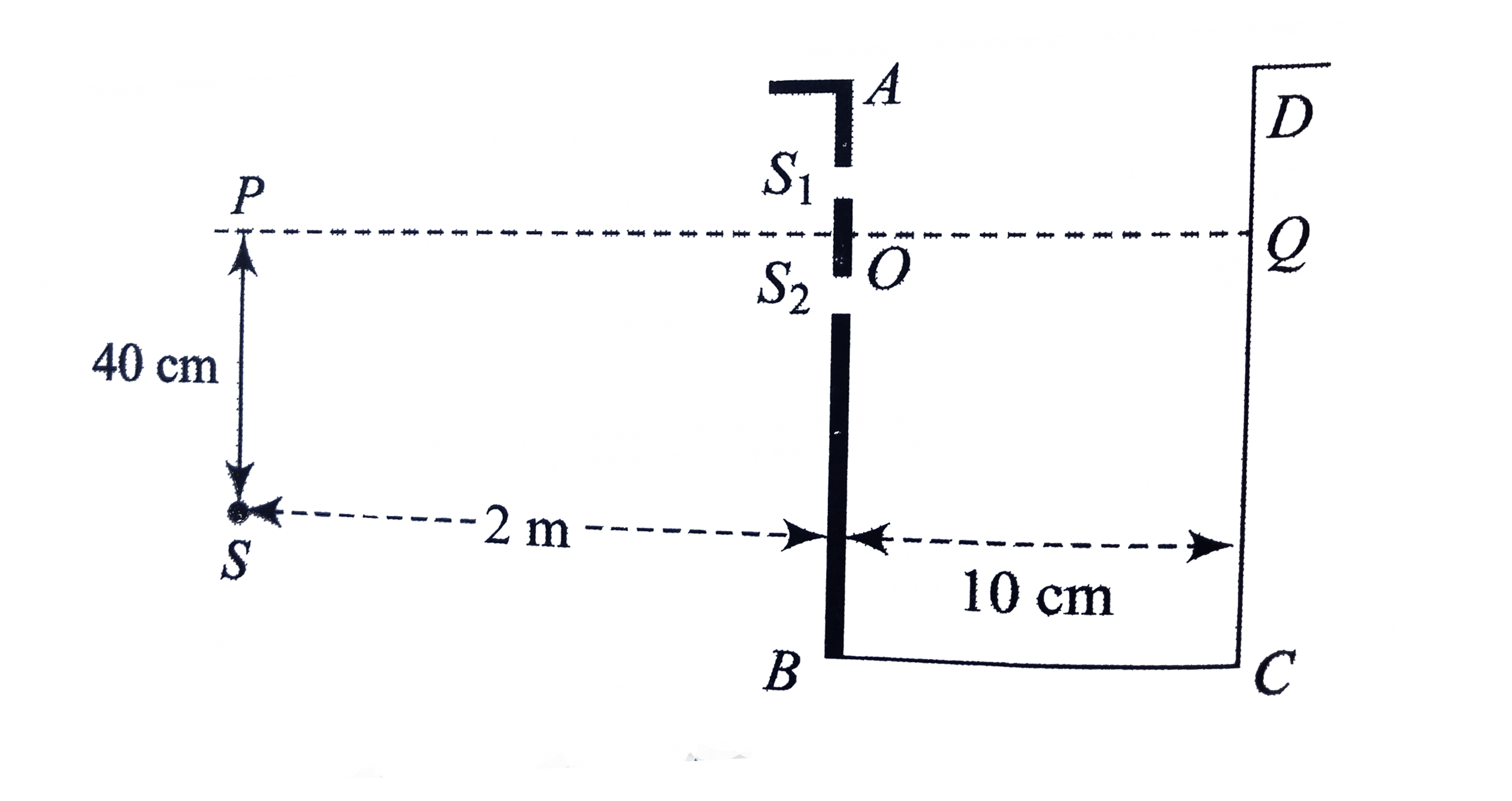
View SolutionA vessel ABCD of 10 cm width has two small slits S1 and S2 sealed with identical glass plates of equal thickness. The distance between the slits is 0.8 mm. POQ is the line peropendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S, 40 cm below P and 2 m form the vessel to illuminate the slits as shown in figure .Calculate the position of the central bright fringe on the other wall CD with respect to line OQ. Now , a liquid is poured into the vessel and filled up to OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid to the liquid.
View SolutionIn Young's double slit experiment, the distance between two slits is made three times then the fringe width will becomes
View SolutionIn a Young's double slit experiment , the path difference at a certain point on the screen ,between two interfering waves is 18th of wavelength .The ratio of the intensity at this point to that at the center of a bright fringe is close to :
View Solution
