How much water should be filled in a container of height 21cm, so that it appears half filled to the observer when viewed from the top of the container (μ=4/3).
8 cm
10.5 cm
12 cm
14 cm
The correct Answer is:D
To solve the problem of how much water should be filled in a container of height 21 cm so that it appears half-filled to an observer when viewed from the top, we can follow these steps:
1. Understanding the Problem:
- We have a container with a total height of 21 cm.
- We need to find the height of water (let's denote it as X) such that when viewed from the top, it appears half-filled.
2. Using the Concept of Apparent Height:
- The refractive index of water (μ) is given as 43.
- When viewed from the top, the apparent height of the water column is given by the formula:
Apparent Height=Xμ
- Since the observer sees the container as half-filled, the apparent height should equal half of the total height of the container:
Xμ=212
3. Setting Up the Equation:
- We can express the equation as:
X43=212
- To eliminate the fraction, we can multiply both sides by 43:
X=212×43
4. Calculating the Value of X:
- Now, simplifying the right side:
X=21×42×3=846=14 cm
5. Conclusion:
- Therefore, the height of water that should be filled in the container is 14 cm.
Final Answer:
The height of water that should be filled in the container is 14 cm.
- We have a container with a total height of 21 cm.
- We need to find the height of water (let's denote it as X) such that when viewed from the top, it appears half-filled.
- The refractive index of water (μ) is given as 43.
- When viewed from the top, the apparent height of the water column is given by the formula:
Apparent Height=Xμ
- Since the observer sees the container as half-filled, the apparent height should equal half of the total height of the container:
Xμ=212
- We can express the equation as:
X43=212
- To eliminate the fraction, we can multiply both sides by 43:
X=212×43
- Now, simplifying the right side:
X=21×42×3=846=14 cm
- Therefore, the height of water that should be filled in the container is 14 cm.
The height of water that should be filled in the container is 14 cm.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question23videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary76videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.710videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY46videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
Similar Questions
How much height of water in cm would be filled in a container of height 14 cm,so that it appears half filled to the observer when viewed from the top of the container (μω=43)
View SolutionA container of height 10 cm is filled with water. There is hole at bottom. Find the pressure difference between point A & B .
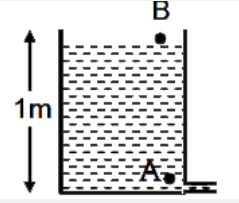 View Solution
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionA liquid is filled in a container to a height H. A small hole is opened in the side of the container a height h below the surface of the liquid. The distance L from the bottom of the container of the point where the stream of liquid leaving the container meets the ground is :
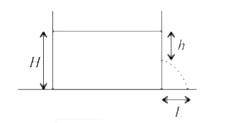 View Solution
View SolutionA beaker contains water up to a height h1 and K oil above water up to another height h2. Find the apparent shift in the position of the bottom of the beaker when viewed from above. Refractive index of water is μ1 and that of K.oil is mu_2.
View SolutionA container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
View SolutionA rectangular container has base of length 12 cm and width 9 cm . A cube of edge 6 cm is placed in the container and then sufficient water is filled into it so that the cube is just submerged . Find the fall in level of the water. In the container , when the cube is removed.
View SolutionAn observer observer a fish moving upwards in a cylindrical container of cross section area 1m2 filled with water up to a height of 5m. A hole is present at the botton of the container having cross section areea 1/1000m2. Find out the speed of the image of fish observed by observer when the botton hole is just opened. (Given: The fish is moving with the speed of 6m/s towards the observer, μ of water =4/3)
View SolutionA fish in water sees an object which is 24cm above the surface of water. The height of the object above the surface of water that will appear to the flash is (μ=4/3)
View Solution

