How much height of water in cm would be filled in a container of height 14 cm,so that it appears half filled to the observer when viewed from the top of the container (μω=43)
The correct Answer is:6
To solve the problem, we need to determine the height of water (h) that needs to be filled in a container of height 14 cm, such that it appears half-filled to an observer looking from the top of the container. Given that the refractive index of water (μ) is 4/3, we can follow these steps:
1. Understand the Problem:
- The total height of the container is 14 cm.
- We need to find the height of water (h) such that it appears half-filled to the observer.
2. Define Apparent Depth:
- When viewed from the top, the apparent depth (d') of the water is given by the formula:
d′=hμ
- Here, μ=43.
3. Calculate Apparent Depth:
- Substitute the value of μ into the formula:
d′=h43=3h4
4. Set Up the Equation:
- For the container to appear half-filled, the apparent depth (d') must equal the height of the container minus the height of the water:
d′=14−h
- Therefore, we can set up the equation:
14−h=3h4
5. Solve for h:
- Rearranging the equation gives:
14=h+3h4
- Combine like terms:
14=4h4+3h4=7h4
- Multiply both sides by 4 to eliminate the fraction:
56=7h
- Now, divide by 7:
h=567=8 cm
6. Conclusion:
- The height of water that needs to be filled in the container is 8 cm.
- The total height of the container is 14 cm.
- We need to find the height of water (h) such that it appears half-filled to the observer.
- When viewed from the top, the apparent depth (d') of the water is given by the formula:
d′=hμ
- Here, μ=43.
- Substitute the value of μ into the formula:
d′=h43=3h4
- For the container to appear half-filled, the apparent depth (d') must equal the height of the container minus the height of the water:
d′=14−h
- Therefore, we can set up the equation:
14−h=3h4
- Rearranging the equation gives:
14=h+3h4
- Combine like terms:
14=4h4+3h4=7h4
- Multiply both sides by 4 to eliminate the fraction:
56=7h
- Now, divide by 7:
h=567=8 cm
- The height of water that needs to be filled in the container is 8 cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIOS)
30 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT TYPE QUESTIOS)
4 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
How much water should be filled in a container of height 21cm, so that it appears half filled to the observer when viewed from the top of the container (μ=4/3).
View SolutionHow much water should be filled in a container of height 21cm, so that it appears half filled to the observer when viewed from the top of the container (μ=4/3).
View SolutionA container of height 10 cm is filled with water. There is hole at bottom. Find the pressure difference between point A & B .
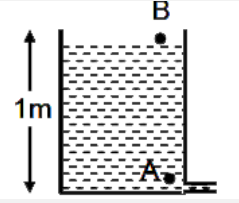
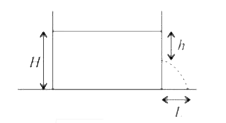
View SolutionA liquid is filled in a container to a height H. A small hole is opened in the side of the container a height h below the surface of the liquid. The distance L from the bottom of the container of the point where the stream of liquid leaving the container meets the ground is :
View SolutionA container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
View SolutionA container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA beaker contains water up to a height h1 and K oil above water up to another height h2. Find the apparent shift in the position of the bottom of the beaker when viewed from above. Refractive index of water is μ1 and that of K.oil is mu_2.
View SolutionA right circular cylinder having diameter 12cm and height 15cm is full of ice-cream. The ice-cream is to be filled in cones of height 12cm and diameter 6cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA cone of a radius 5 cm is filled with water. If the water poured in a cylinder of radius 10cm, the height of the water rises 2 cm, find the height of the cone.
View Solution
