The curve of blinding energy per nucleon as a function of atomic mass number has a sharp peak for helium nucleus. This implies that helium.
can easily be broken up
is very stable
can be used as fissionable material
is radioactive
The correct Answer is:B
To solve the question regarding the binding energy per nucleon and its implications for the helium nucleus, we can follow these steps:
1. Understanding Binding Energy per Nucleon:
- The binding energy per nucleon is a measure of the stability of a nucleus. It indicates how much energy is required to remove a nucleon from the nucleus. A higher binding energy per nucleon means a more stable nucleus.
2. Analyzing the Curve:
- The question mentions a curve of binding energy per nucleon as a function of atomic mass number (A). This curve typically shows that as we move from lighter to heavier nuclei, the binding energy per nucleon increases, reaches a peak, and then starts to decrease for very heavy nuclei.
3. Identifying the Peak for Helium:
- The sharp peak for helium indicates that it has a significantly higher binding energy per nucleon compared to its neighboring nuclei (like hydrogen and lithium). This sharp peak suggests that helium is particularly stable.
4. Implications of Stability:
- Since helium has a high binding energy per nucleon, it implies that helium nuclei are tightly bound and thus very stable. This stability means that helium is less likely to undergo radioactive decay or fission.
5. Conclusion:
- Therefore, the implication of the sharp peak in the binding energy per nucleon curve for helium is that helium is very stable compared to its neighboring elements. It does not easily break apart, and it is not a fissionable material.
Final Answer:
Helium is very stable compared to its neighboring nuclei due to its high binding energy per nucleon, as indicated by the sharp peak in the binding energy curve.
---
- The binding energy per nucleon is a measure of the stability of a nucleus. It indicates how much energy is required to remove a nucleon from the nucleus. A higher binding energy per nucleon means a more stable nucleus.
- The question mentions a curve of binding energy per nucleon as a function of atomic mass number (A). This curve typically shows that as we move from lighter to heavier nuclei, the binding energy per nucleon increases, reaches a peak, and then starts to decrease for very heavy nuclei.
- The sharp peak for helium indicates that it has a significantly higher binding energy per nucleon compared to its neighboring nuclei (like hydrogen and lithium). This sharp peak suggests that helium is particularly stable.
- Since helium has a high binding energy per nucleon, it implies that helium nuclei are tightly bound and thus very stable. This stability means that helium is less likely to undergo radioactive decay or fission.
- Therefore, the implication of the sharp peak in the binding energy per nucleon curve for helium is that helium is very stable compared to its neighboring elements. It does not easily break apart, and it is not a fissionable material.
Helium is very stable compared to its neighboring nuclei due to its high binding energy per nucleon, as indicated by the sharp peak in the binding energy curve.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - B Medical entrance special format questions9videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - MATCH THE COLUMNS4videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - CHECK POINT 13.315videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective10videos
MODERN PHYSICS - 2
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary76videos
RAY OPTICS
Similar Questions
The graph between the binding energy per nucleon (E) and atomic mass number (A) is as-
View SolutionUsing the curve for the binding energy per nucleon as a function of mass number A, state clearly how the release in energy in the processes of nuclear fission and nuclear fusion can be explained.
View SolutionFind the binding energy per nucleon of 79^197Au if its atomic mass is 196.96 u.
View SolutionDraw a plot of the binding energy per nucleon as a function of mass number for a large number of nuclei , 2≤A≤240 . How do you explain the constancy of binding energy per nucleon in the range 30<A<170 using the property that nuclear force is short-ranged ?
View SolutionAssertion : Binding energy per unit nucleon increase in atomic mass number .
Reason : Density of nucleus increases with increase in mass number.View SolutionDraw the graph showing thervariation of binding energy per nucleon with mass number. Give therason for the decrease of binding energy per nucleon for nuclei with high mass numbers.

The binding energy per nucleon for nuclei with high mass number is low due to the large coulomb repulsion between the protons inside these nuclei.View SolutionAssertion The binding energy per nucleon, for nuclei with atomic mass number A>100, decreases with A.
Reason The nuclear forces are weak for heavier nuclei.View SolutionAs the mass number A increases, the binding energy per nucleon in a nucleus.
View SolutionThe dependence of binding energy per nucleon, BN on the mass number, A is represented by.
(a)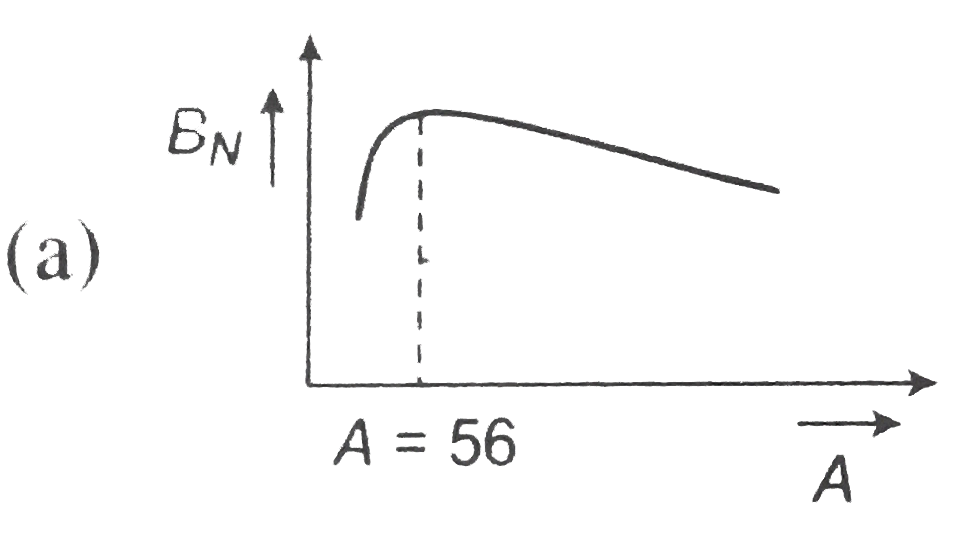 , (b)
, (b) 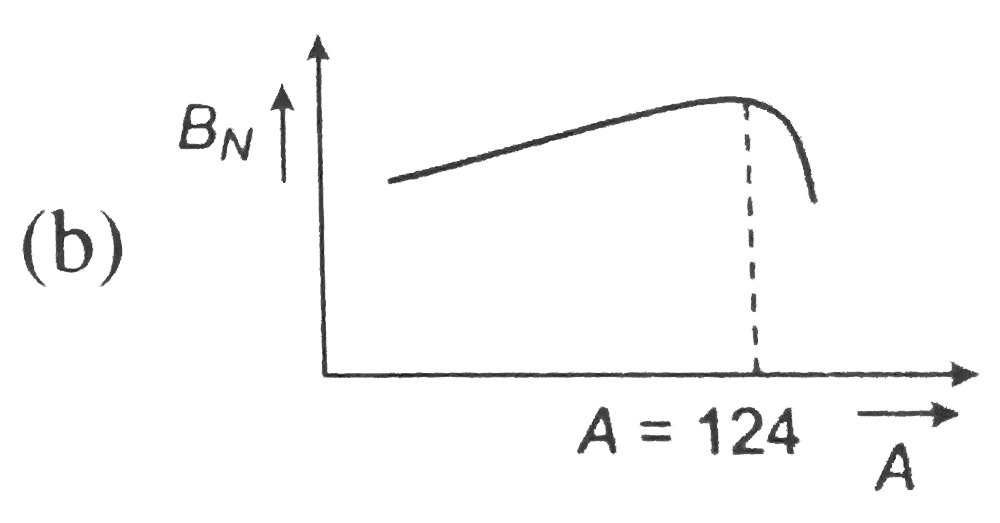 ,
,
( c)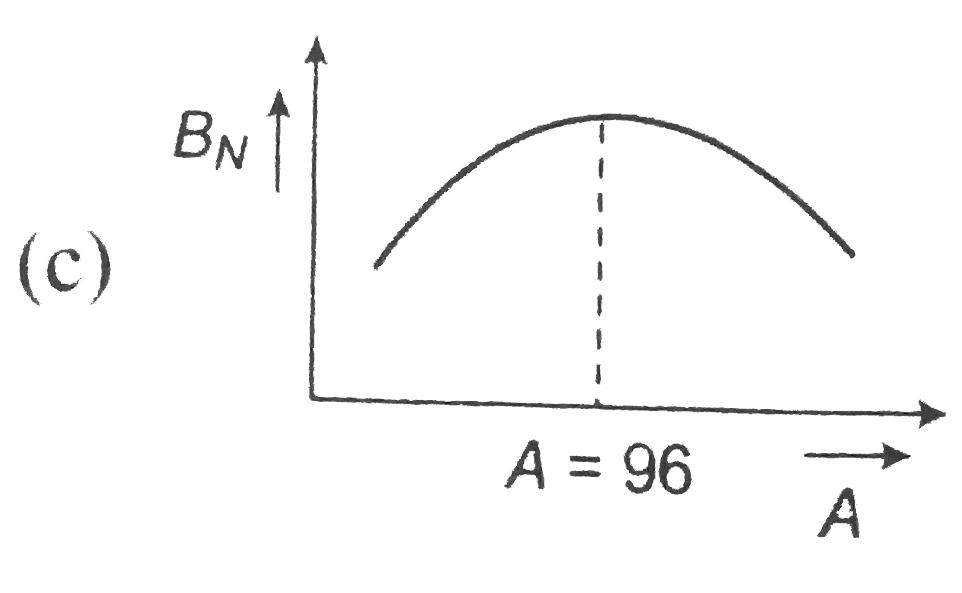 , (d)
, (d) 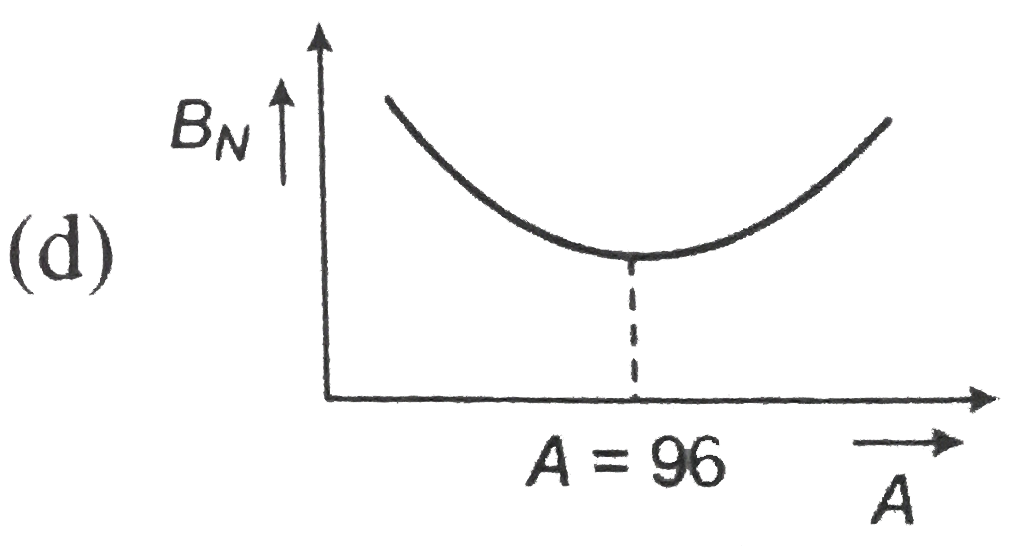 .View Solution
.View SolutionThis binding energy per nucleon for the parent nucleus is E1 and that for the daughter nuclei is E2. Then
View Solution

