The gravitational force between a H-atom and another particle of mass m will be given by Newton's law: F=GM.mr2, where r is in km and
M=mproton+melectron
M=mproton+melectron−Bc2(B=13.6eV)
M is not relate to the mass of the hydrogen atom
M=mproton+melectron−|V|c2(|V| = magnitude of the potential energy of electron in the H-atom)
The correct Answer is:B
Given, FGMmr2, where
M = effective mass of hydrogen atom = mass of electron + mass of proton −(B2/c2) where, B is BE hydrogen atom = 13.6 eV
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - B Medical entrance special format questions9videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - MATCH THE COLUMNS4videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - CHECK POINT 13.315videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective10videos
MODERN PHYSICS - 2
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary76videos
RAY OPTICS
Similar Questions
Assertion : Mass of the rod AB is m1 and of particle P is m2. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
F=Gm1m2r2
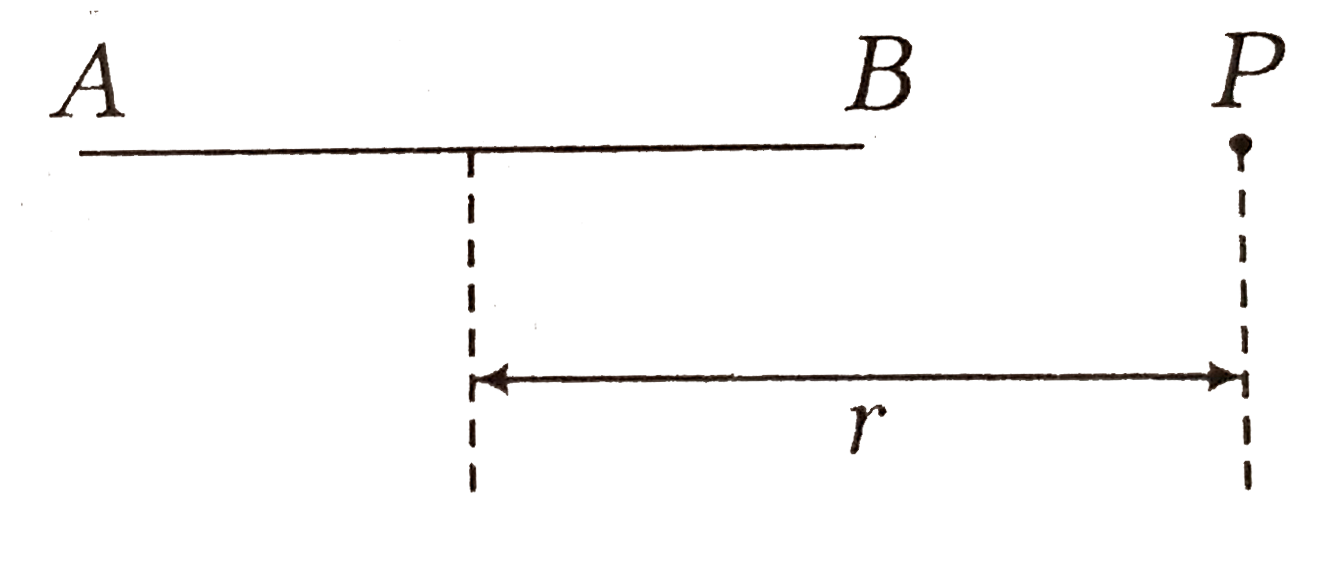
Reason : The relation F=Gm1m2r2 can be applied directly only to find force between two particles.View SolutionAssertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.View Solution
Knowledge Check
- Question 1 - Select One
The gravitational force F between two masses m1andm2 separeted by a distance r is given by
F=Gm1m2r2
Where G is the universal gravitational constant. What are the dimensions of G ?AM−1L2T−3BM−1L3T−2CML3T−2DML2T−3 - Question 2 - Select One
Two sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
A3FBFCF3DF9
If gravitational attraction between two points masses be given by F=Gm1m2rn. Then the period of a satellite in a circular orbit will be proportional to
View SolutionTwo sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
View SolutionTwo sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
View SolutionThe gravitational force between two objects is proportional to 1/R (and not as 1/R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
View SolutionThe gravitational force between two objects is proportional to 1/R (and not as 1/R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
View SolutionStatement I: The force of gravitation between a sphere and a rod of mass M2 is =(GM1M2)/r.
Statement II: Newton's law of gravitation holds correct for point masses.
 View Solution
View Solution

