What is the minimum thickness of a thin film (μ=1.2) that results in constructive interference in the reflected light? If the film is illuminated with light whose wavelength in free space is λ=500nm ?
104 nm
200 nm
300 nm
400 nm
The correct Answer is:A
To find the minimum thickness of a thin film that results in constructive interference in the reflected light, we can follow these steps:
Step 1: Understand the Condition for Constructive Interference
For a thin film with a refractive index μ, the condition for constructive interference in reflected light (when the film is illuminated from air) is given by the formula:
2μt=(n−12)λ
where n is an integer (1, 2, 3, ...), t is the thickness of the film, and λ is the wavelength of light in vacuum.
Step 2: Set Up for Minimum Thickness
To find the minimum thickness, we set n=1:
2μt=(1−12)λ
This simplifies to:
2μt=12λ
Step 3: Solve for Thickness t
Now, we can rearrange the equation to solve for t:
t=λ4μ
Step 4: Substitute Given Values
We know:
- λ=500nm=500×10−9m
- μ=1.2
Substituting these values into the equation:
t=500×10−94×1.2
Step 5: Calculate the Thickness
Calculating the denominator:
4×1.2=4.8
Now substituting back:
t=500×10−94.8≈104.17×10−9m
Converting to nanometers:
t≈104.17nm
Step 6: Round the Result
Rounding to the nearest whole number, we get:
t≈104nm
Final Answer
The minimum thickness of the thin film that results in constructive interference in the reflected light is approximately 104 nm.
---
For a thin film with a refractive index μ, the condition for constructive interference in reflected light (when the film is illuminated from air) is given by the formula:
2μt=(n−12)λ
where n is an integer (1, 2, 3, ...), t is the thickness of the film, and λ is the wavelength of light in vacuum.
To find the minimum thickness, we set n=1:
2μt=(1−12)λ
This simplifies to:
2μt=12λ
Now, we can rearrange the equation to solve for t:
t=λ4μ
We know:
- λ=500nm=500×10−9m
- μ=1.2
t=500×10−94×1.2
Calculating the denominator:
4×1.2=4.8
Now substituting back:
t=500×10−94.8≈104.17×10−9m
Converting to nanometers:
t≈104.17nm
Rounding to the nearest whole number, we get:
t≈104nm
The minimum thickness of the thin film that results in constructive interference in the reflected light is approximately 104 nm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - taking it together
47 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion reason
8 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced E. Integer Type Questions
13 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
Similar Questions
Calculate the minimum thickness of a soap bubble film (μ=1.33)that results in constructive interference in the reflected light if the film is illuminated with light whose wavelength in free space is λ=600nm.
View SolutionWhat is the minimum thickness of thin film required for constructive interference in the reflected light through it ?
(Given, the refractive index of the film =1.5, wavelength of the lilght incident on the film =600 nm.
View Solution
Knowledge Check
What is the minimum thickness of a soap bubble needed for constructive interference in reflected light, if the light incident on the film is 750 nm? Assume that the refractive index for the film is n=1.33
A282 nmB70.5 nmC141 nmD387 nmThe colours seen in the reflected white light from a thin oil film are due to
ADiffractionBInterferenceCPolarisationDDispersion
What is the minimum thickness of a soap bubble needed for constructive interference in reflected light, if the light incident on the film is 750 nm? Assume that the refractive index for the film is n=1.33
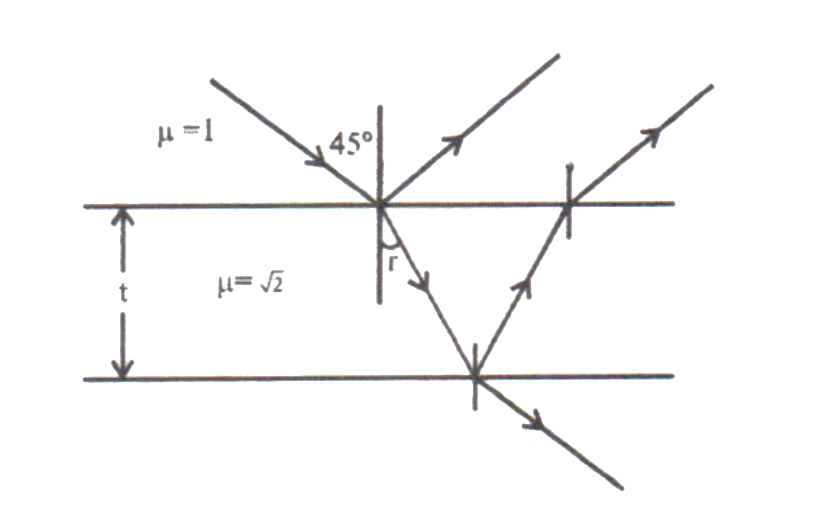
View SolutionA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
View SolutionAn oil film covers the surface of a small pond. The refractive index of the oil is greater than that of water. At one point on the film, the film has the smallest non-zero thickness for which there will be destructive interference in the reflected light when infrared radiation with wavelength 800 nm is incident normal to the film. When this film is viewed at normal incidence at this same point, for what visible wavelengths, if any, will there be constructive interference? (Visible light has wavelengths between 400nm and 700 nm )
View SolutionTwo slits spaced 0.450nm apart are placed 75.0 cm from a screen. What is the distance between the second and third dark lines of the interference pattern on the screen when the slits are illuminated with coherent light with a wavelength of 500nm?
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.38. The smallest thickness of the film that gives an interference maxima in the reflected light when light of wavelength 5520 Å falls at normal incidence is
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.34. Find the smallest thickness of the film that gives in interference maximum in the reflected light when light of wavelength 5360Å fall at normal incidence.
View Solution
