For small deformations stress is directly proportional to strain.
for small deformations, stress is directly proportional to strain.
Similar Questions
Knowledge Check
For a steel wire, stress is directly proportional to strain. This is possible only when
Athe wire undergoes plastic deformation.Bwire is loaded till the breaking point.Cwire is loaded till the elastic limit.Dwire exhibits neck formation.Assertion : For small deformations, the stress and strain are proportional to each other.
Reason: A class of solids called elastomers does not obey Hooke's law.ABoth assertion and reason are true and reason is the correct explanation of assertion.BBoth assertion and reason are true but reason is not the correct explanation of assertion.CAssertion is true but reason is false.DBoth assertion and reason are false.Within the elastic limit, stress is directly proportional to strain produced in a body is the statement of
ARobert's lawBHooke's lawCNewton's lawDBoyle's law
Statement-1 : The value of moduli of elasticity is directly proportional to stress.
Statement-2 : The value of moduli of elasticity is inversely proportional to strain.
Statement-3 : The value of moduli of elasticiy is independent of magnitude of stress and strain.
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
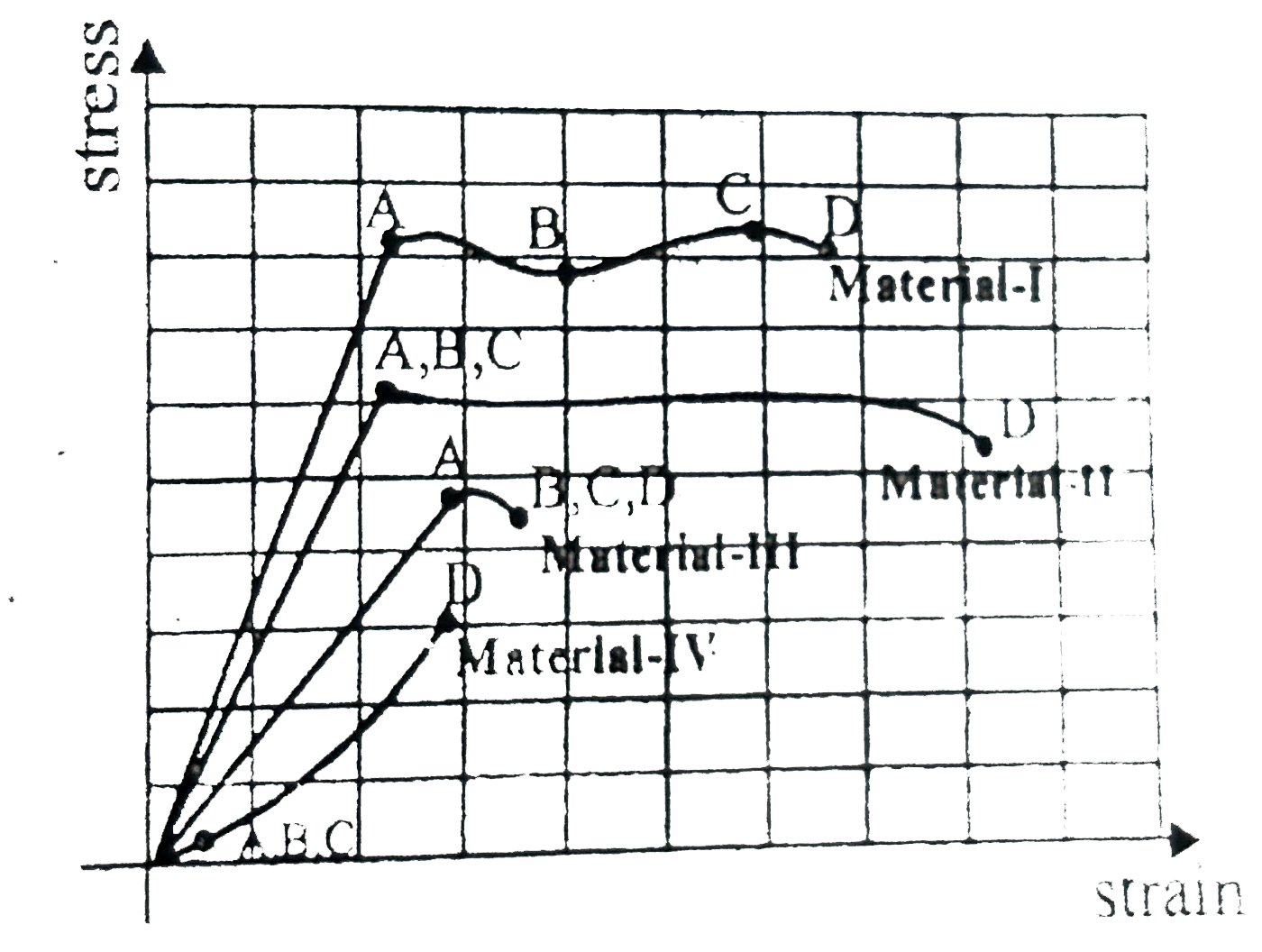
Material which is good for making wires by stretching is
View SolutionStatement-1 : The value of moduli of elasticity is directly proportional to stress.
Statement-2 : The value of moduli of elasticity is inversely proportional to strain.
Statement-3 : The value of moduli of elasticiy is independent of magnitude of stress and strain.
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

Material which is good for making wires by stretching is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.
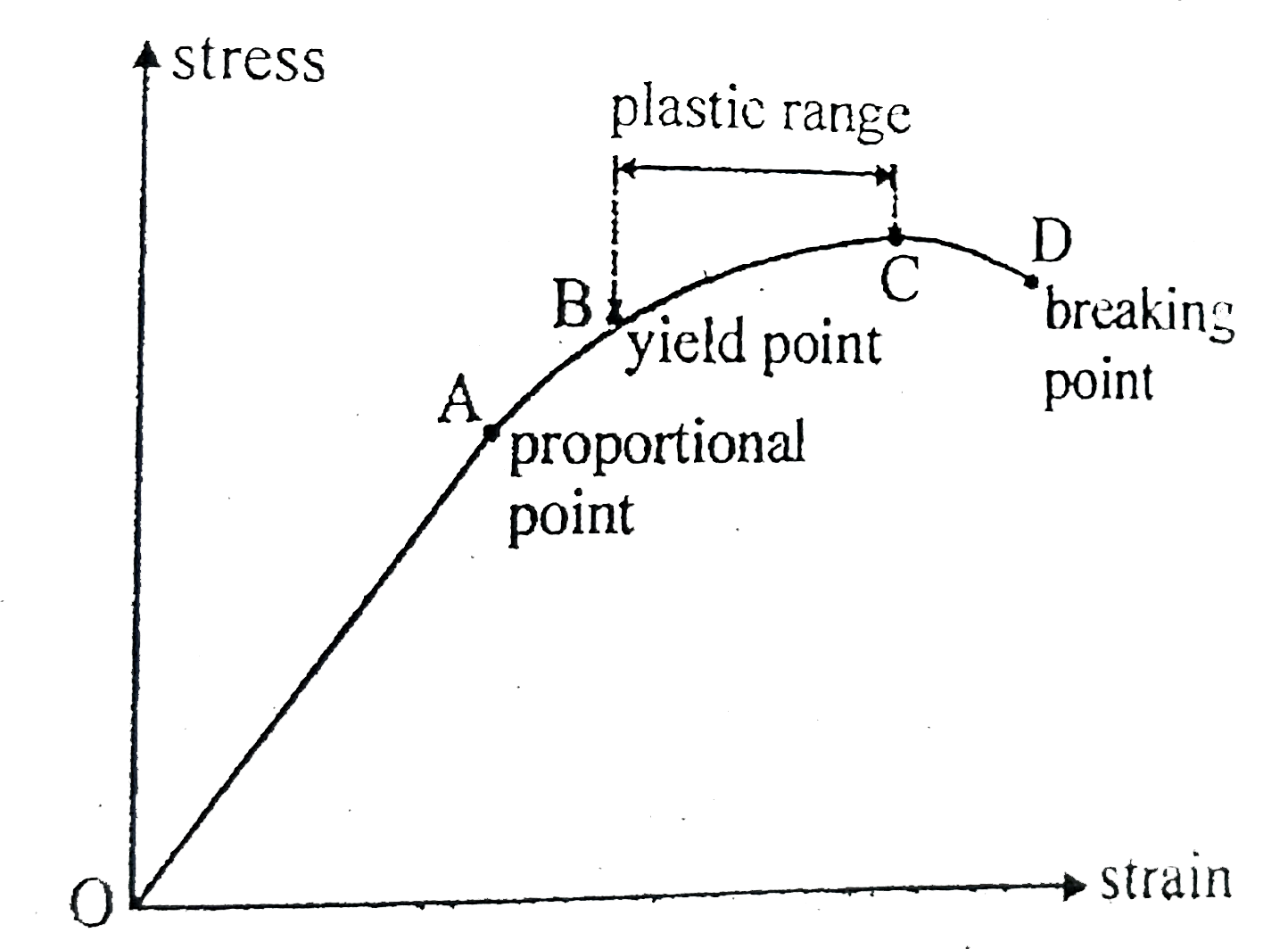
Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
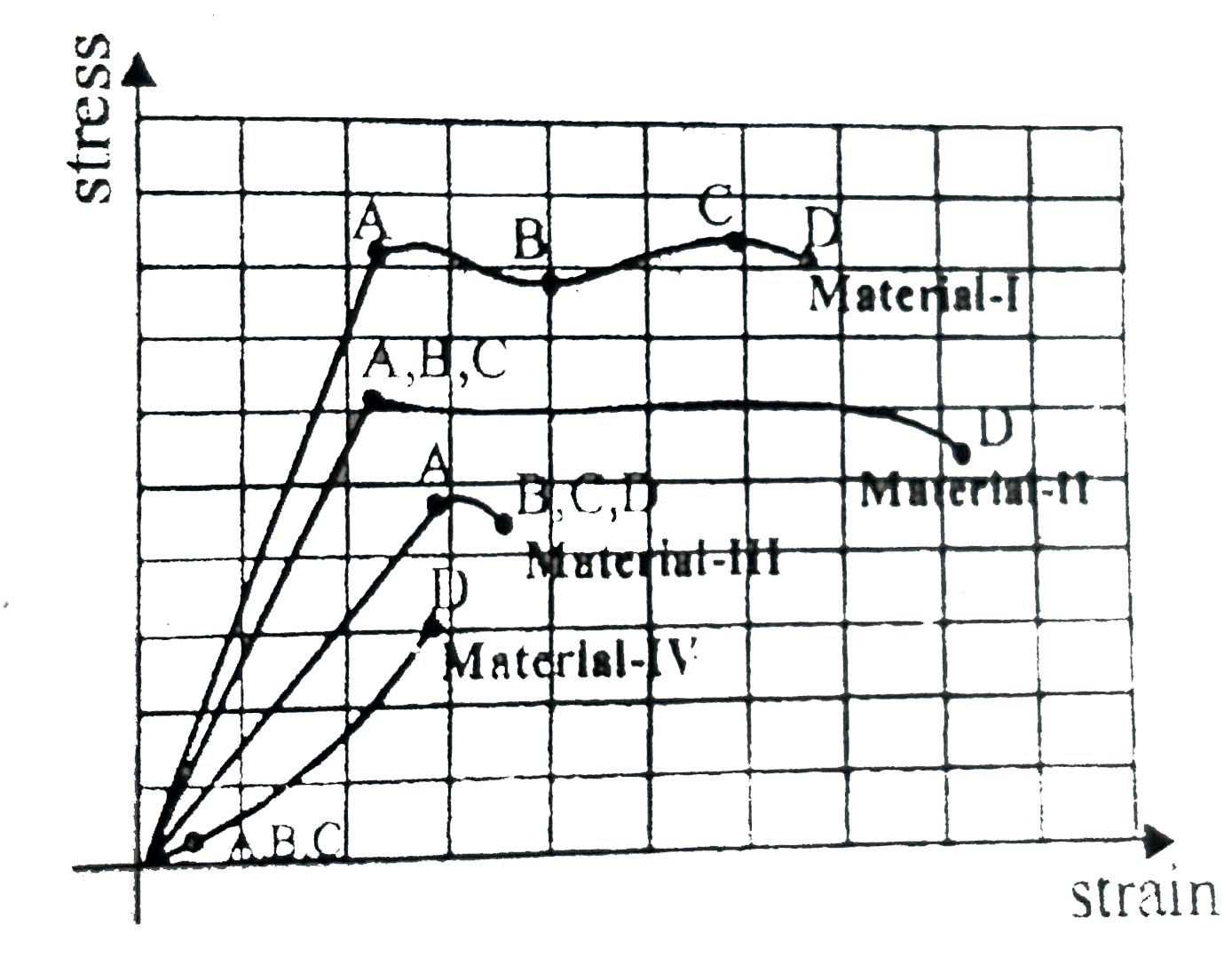
Material which is most brittle is
View Solution
