A particle moving along a straight line has the relation s=t2+3, connecting the distance s described by the particle in time 1. Find the velocity and acceleration of the particle at t=4 seconds.Solution in Telugu
The correct Answer is:50 units/sec, 24units/sec2
Step by step video, text & image solution for A particle moving along a straight line has the relation s =t^2 +3, connecting the distance s described by the particle in time 1. Find the velocity and acceleration of the particle at t=4 seconds. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RATE OF CHANGEBOOK - AAKASH SERIESCHAPTER - RATE OF CHANGEEXERCISE - Exercise 6.1 (SHORT ANSWER QUESTIONS)-II
12 Videos
- RATE OF CHANGEBOOK - AAKASH SERIESCHAPTER - RATE OF CHANGEEXERCISE - Advanced Subjective Type Questions
22 Videos
- RATE OF CHANGEBOOK - AAKASH SERIESCHAPTER - RATE OF CHANGEEXERCISE - Advanced Analytical Solved Examples
3 Videos
- RATE MEASUREMENTBOOK - AAKASH SERIESCHAPTER - RATE MEASUREMENTEXERCISE - PRACTICE SHEET (EXERCISE - 1) (LEVEL - 1) (STRAIGHT OBJECTIVE TYPE QUESTION)
43 Videos
- REAL FUNCTIONS BOOK - AAKASH SERIESCHAPTER - REAL FUNCTIONS EXERCISE - EXERCISE-1
34 Videos
Similar Questions
A point P is moving on the curve y=2x2 . The x coordinate of P is increasing at the rate of 4 units per second . Find the rate at which y coordinate is incerasing when the point is at (2,8).
View SolutionA stone is dropped into a quiet pond and waves move in circles outward from the place where it strikes, at a speed of 30 cm per second. At the instant when the radius of the wave ring is 50 mt, find the rate of increase in the area and in the circumference of the wave ring.
View SolutionOn the curve x3=12y, find the interval of value of x for which the abscissa changes at a faster rate than the ordinate?
View SolutionIf a particle moves alonga straight line by S=4t2−8t+3 and the time at which the particle comes of rest is 't' seconds then '2t' is
View SolutionFind the domains of the following functions
f(x)=x2+x+1
View SolutionThe acceleration of a particle moving along a straight line is (6t^(2)-3t)cm/s^(2), at time t seconds,If the velocity of the particle at time 2 seconds be 10cm/s ,find its veloctiy at time t seconds.
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at the origin .
View SolutionA particle moves along a straight line such that its displacement s at any time t is given by s=t3−6t2+3t+4m, t being is seconds. Find the velocity of the particle when the acceleration is zero.
View SolutionA particle moves in a straight line with an acceleration a ms^-2 at time 't' seconds where a = - (1)/(t^2) When t = 1 the particle has a velocity of 3 ms^-1 . Find the velocity of the particle at t = 4 s .
View SolutionA particle moves in a straight line as s =alpha(t-4)+beta(t-4)^(2) . Find the initial velocity and acceleration.
View Solutionसरल रेखा में गतिमान एक कण का त्वरण (a) समय (t) ग्राफ संलग्न चित्र में प्रदर्शित है। कण का प्रारम्भिक वेग 2 मीटर/सेकण्ड है। ज्ञात कीजिए (i) t=3 सेकण्ड तथा t=6 सेकण्ड पर कण का वेग (ii) t=0 से t=6 सेकण्ड के बीच कण का औसत त्वरण।
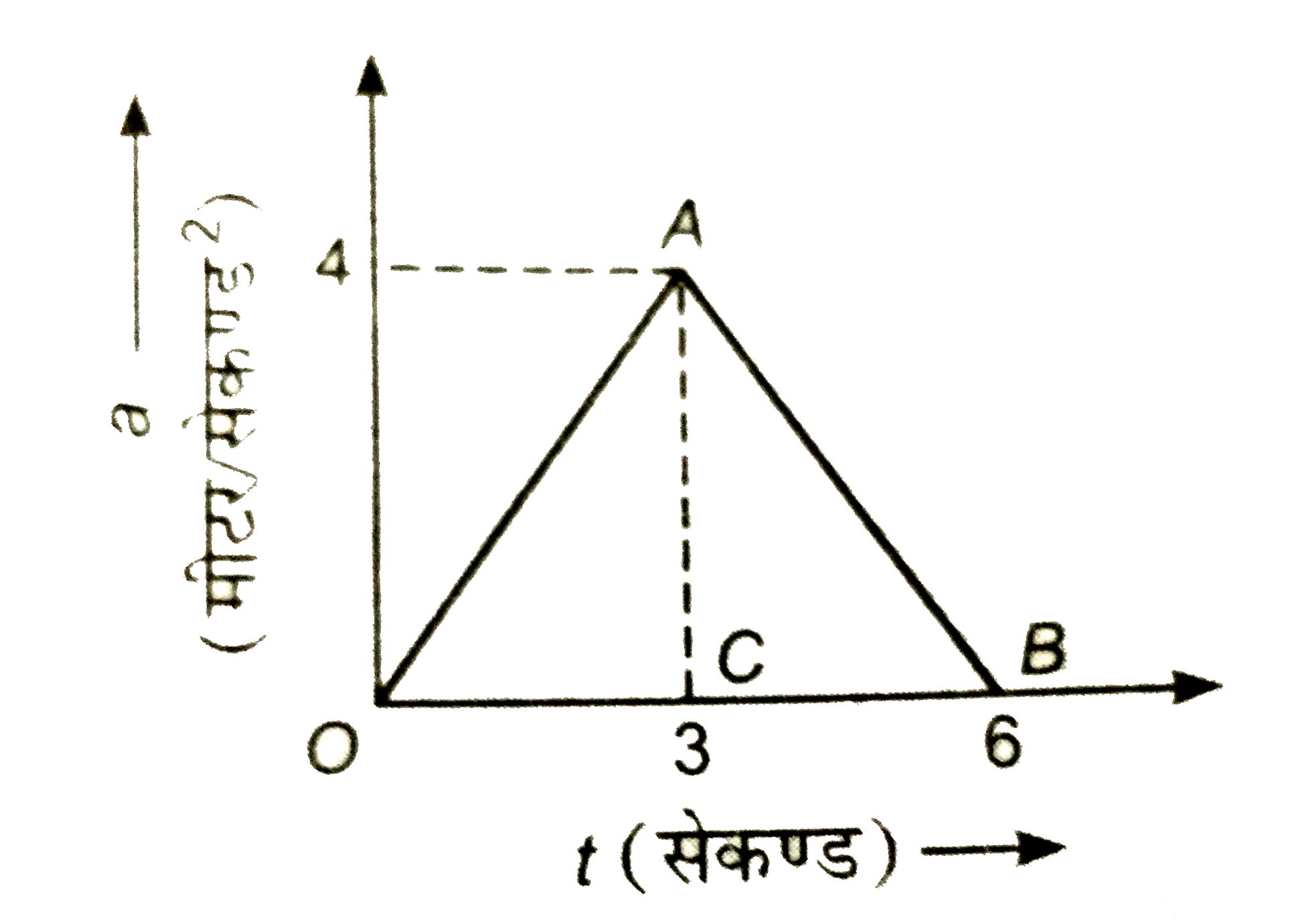
View SolutionThe acceleration of a particle moving along a straight line is (6t2−3t)cm/s2, at time t seconds. If the velocity of the particel at time 2 seconds be 10cm/s, find its velocity at time t seconds.
View SolutionA particle moving along a straight line has the relation s=t3+2t+3, connecting the distance s describe by the particle in time t. Find the velocity and acceleration of the particle at t=4 sec.
View Solution[" A particle is moving along "],[" a straight line with non- "],[" uniform acceleration.The "],[" displacement of the "],[" particle is given by "],[S=2t^(3)+3t^(2)+5t" where "S" is in "],[" metres and "t" is in seconds."],[" The velocity of the particle "],[" at "t=2" seconds is "]
View Solutionएक कण सरल रेखा में गति कर रहा है । t समय पर कण द्वारा चली गई दुरी x निम्न संबंध द्वारा दी जाती है -
x=4t2+2t
समय t=12 पर कण का वेग ज्ञात कीजिए ।
View Solution[" A particle is moving along "],[" a straight line with non- "],[" uniform acceleration.The "],[" displacement of the "],[" particle is given by "],[S=2t^(3)+3t^(2)+5t" where "S" is in "],[" metres and "t" is in seconds."],[" The velocity of the particle "],[" at "t=2" seconds is "]
View Solution
