Question

Explain formation of face centred cubic unit cell and hexagonal close packing in three dimensions.

Explanation

In hexagonal close packing layer in two dimensions, there are two sets of triangular voids. The three dimensional arrangement is obtained by stacking the two dimensional hexagonal layers one above the other.

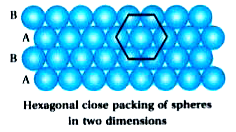
Over the first layer (say "A") of two dimensional hexagonal arrangement, if the second layer (say "B") is placed, the one set of triangular void of layer "A" is covered by the spheres of layer "B".  

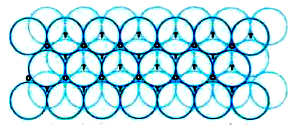
Over the second layer "B", there are again two sets of triangular voids. If the third layer is placed over the triangular voids of second layer such that the spheres of third layer an first layer in exact alignment, the hexagonal close packing in three dimensional is obtained.

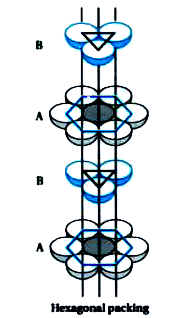
The third layer and first layer are exactly same and hence it is called "A" type. Thus the arrangement obtained is ABABAB.... Pattern.
Ex. : Zn and Mg shows this type of arrangement.
.
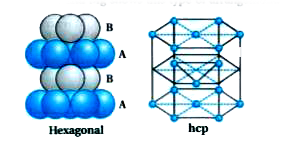If the third layer of the spheres are placed over the triangular voids of the second layer that are formed just above the unoccupied voids of the first layer, the face cubic centred unit cell is formed.
The third layer is different from layers A and B. Hence, if the third layer is called "C", the arrangement obtained is ABCABCABC... ie., fourth layer of sphere and first layer of spheres are exactly same.

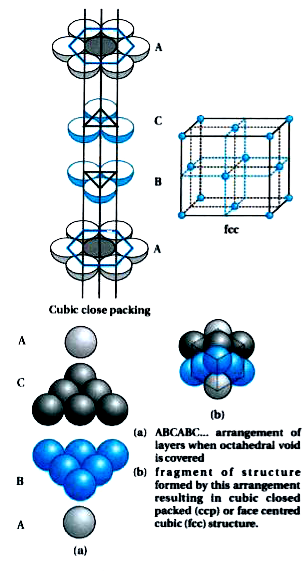
Ex. : Metals such as Cu, Ag, etc. crystallizes in FCC structure.  
In both type of close packing structures, the packing efficiency is 74% and co-ordination number is 12.`