If O is the point inside the triangle ABC such that ⌊OBC=A/2,⌊OCA=B/2,⌊OAB=C/2 then Sin(A−C/2)Sin(B−C/2).Sin(C−B/2)SinA/2.SinB/2.SinC/2 = Solution in Telugu
1
2
3
4
The correct Answer is:A
Step by step video, text & image solution for If O is the point inside the triangle ABC such that lfloor OBC = A//2, lfloor OCA = B//2 , lfloor OAB = C//2 then (Sin(A -C//2)Sin(B-C//2).Sin(C-B//2))/(Sin A//2 . Sin B//2.SinC//2) = by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - I (More than One correct answer Type Questions)4videos
PROPERTIES OF TRIANGLES
- BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - I (Matrix Matching Type Questions)1videos
PROPERTIES OF TRIANGLES
- BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - PRACTICE EXERCISE132videos
PROPERTIES OF TRIANGLES
- BOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS30videos
PLANES
- BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES55videos
PROPERTIES OF VECTORS
Similar Questions
If the sines of the angle A and B of a triangle ABC satisfy the equation c2x2−c(a+b)x+ab=0 . Then the triangle
09:02View SolutionIn a ΔABC,BC=2,CA=1+√3 and ∠C=60∘. Feet of the perpendicular from A, B and on the opposite sides BC, CA and AB are D, E and F respectively and perpendiculars are concurrerant at P.
Now match the entries of Column-I with respective entries of column-II.
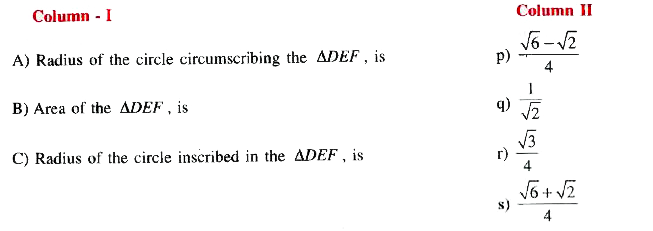 03:55View Solution
03:55View SolutionIf a = 3, b =4 , sin A = 3/4 then ∠B=
05:19View SolutionThe plane 2x + 3y + kz - 7 = 0 is parallel to the line whose d.r's are (2,-3,1) then k=
03:52View SolutionIf ¯¯¯¯¯¯OA=¯i+2¯j−3¯k,¯¯¯¯¯¯OB=3¯i−2¯j+5¯kand2¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB then ¯¯¯¯¯¯AC=
03:04View SolutionIn any triangle ABC, prove that: a2sin(B−C)sinB+sinC+b2sin(C−A)sinC+sinA+c2sin(A−B)sinA+sinB=0
03:52View SolutionIn a ΔABC, SinASinC=sin(A−B)sin(B−C) , then a2,b2,c2 are in
04:15View SolutionIn a ΔABC if a2sin(B−C)+b2sin(C−A)+c2sin(A−B)=0, then triangle is
06:35View SolutionIn Delta ABC if sin^(2)((A)/(2)),sin^(2)((B)/(2)),sin^(2)((C)/(2)) are in H.P then a,b,c will be in ,sin^(2)((C)/(2))
06:03View SolutionIn any ΔABC, prove that : a2sin(B−C)sinB+sinC+b2sin(C−A)sinC+sinA+c2sin(A−B)sinA+sinB=0
View SolutionΔABC में सिद्ध कीजिए कि -
Δ=b2−c22⋅sinBsinCsin(B−C)02:53View SolutionIn Delta ABC, if sin^2""A/2, sin^2""B/2,sin^2""C/2 are in H.P, then a,b,c in
02:48View SolutionIn Delta ABC, if sin A: sin C=sin (A-B): sin (B-C) , then a^2,b^2,c^2 are in
04:18View SolutionIn any triangle ABC prove that a2sin(B−C)sinA+b2sin(C−A)sinB+c2sin(A−B)sinC=0
View Solutionif O is the point inside the triangle ABC such that ∠OBC=A2,∠OCA=B2,∠AOB=C2, then sin(A−C2)sin(B−A2)sin(C−B2)sinA2sinB2sinC2 equal :
07:16View Solution

