In a $Δ A B C, B C = 2, C A = 1 + \sqrt{3} and ∠ C = 60^{\circ}$ . Feet of the perpendicular from A, B and on the opposite sides BC, CA and AB are D, E and F respectively and perpendiculars are concurrerant at P.
Now match the entries of Column-I with respective entries of column-II.

Text Solution

Verified by Experts

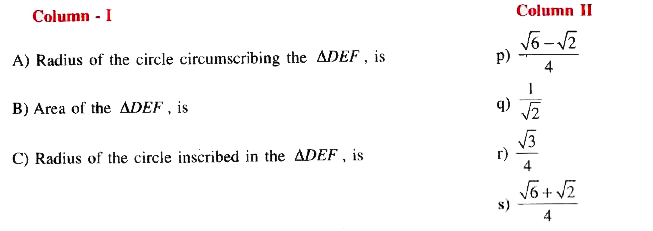
The correct Answer is:A, B, C

Updated on:21/07/2023

The in circle of $Δ A B C$ touches the sides BC, CA and AB at D, E and F respectively. Then AF + BD + CE is equal to :
A $\frac{1}{2}$ (Perimeter of $Δ$ ABC)
B $\frac{1}{3}$ (Perimeter of $Δ$ ABC)
C $\frac{1}{4}$ (Perimeter of $Δ$ ABC)
DPerimeter of $Δ$ ABC
In a $Δ A B C$ right angle at C .P is the length of $⊥$ from C to AB. If a, b, c, are the length of BC , CA, AB. Which relation is correct .
A $\frac{1}{p^{2}} = \frac{1}{b^{2}} - \frac{1}{a^{2}}$
B $\frac{1}{p^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$
C $\frac{1}{p^{2}} + \frac{1}{a^{2}} = - \frac{1}{b^{2}}$
D $\frac{1}{p^{2}} = \frac{1}{a^{2}} - \frac{1}{b^{2}}$
In a $Δ A B C, D, E, F$ are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A $- - \to B E + - - \to C F$
B $- - \to B E - - - \to C F$
C $- - \to C F - - - \to B E$
D $- - - \to B E - - - \to C F$