The distance from a point A to a line BC is 3. Two lines L and L' parallel to ¯¯¯¯¯¯BC, divide Δle ABC into three parts of equal area as shown in the figure then distance between L and L'.
√4−√3
√6−√3
√3−√6
√3−√2
The correct Answer is:B
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - II(More than One correct answer Type Questions)
3 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - II(Matrix Matching Type Questions)
5 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - I (Linked Comprehension Type Questions)
3 Videos
- PLANESBOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
Similar Questions
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
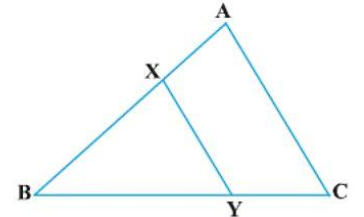
View SolutionThe area of a triangle ABC is 63 sq. units. Two parallel lines DE, FG, are drawn such that they divide the line segments AB and BC into three equal parts. What is the area of the quadrilateral DEGF ?
View Solution
Knowledge Check
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
A√2+1+√2B2−√2:2C1:√2D1:1If distance of a point (x1,y1) from each of two lines L1 and L2, through the orign , is δ, then joint equation of L1 and L2 is
A(x1y−xy1)2=δ2(x2+y2)B(x1y+xy1)2=δ2(x2+y2)C(x1x−yy1)2=δ2(x2+y2)D(xx1+yy1)2=δ
l and m are two parallel lines intersected by another pair of parallel lines p and q as shown in figure. Show that ABC≅CDA.

View SolutionThe line L is given by 2x+by=7, passes through (8, 3). The line K is parallel to L and has the equation cx−3y=c. Find the distance between L and K.
View SolutionFind the distance of the point P from the line l in that : l:xa−yb=1andP≡(b,a)
View SolutionFind the distance of the point P from the line l in that : l:xa−yb=1andP≡(b,a)
View SolutionConsider a triangle ABC with AB=13, BC=14, CA=15. A line perpendicular to BC divides the interior of ΔABC into two regions of equal area. Suppose that the aforesaid perpendicular cuts BC at D, and cuts ΔABC again at E. If L is the length of the line segment DE, find L2.
View SolutionFind the distance of the point P from the line l in that : l:12x−7=0≡(3,−1)
View Solution
