The area of a triangle ABC is 63 sq. units. Two parallel lines DE, FG, are drawn such that they divide the line segments AB and BC into three equal parts. What is the area of the quadrilateral DEGF ?
28 sq units
35 sq units
21 sq units
48 sq units
To find the area of the quadrilateral DEGF formed by the two parallel lines DE and FG that divide the triangle ABC into three equal parts, we can follow these steps:
1. Understand the Triangle Division:
The triangle ABC has an area of 63 square units. The lines DE and FG divide the segments AB and BC into three equal parts. This means that the height from point C to line AB is divided into three equal segments.
2. Determine the Areas of Smaller Triangles:
When the triangle is divided by the lines DE and FG, it creates smaller triangles ACD and BCF. The area of these smaller triangles can be determined by the ratio of their heights to the height of triangle ABC.
3. Calculate the Area of Triangle ACD:
Since DE is the first line dividing the triangle, it is at one-third the height of triangle ABC. The area of triangle ACD can be calculated as:
Area of ACD=13×Area of ABC=13×63=21 sq. units
4. Calculate the Area of Triangle BCF:
The line FG is at two-thirds the height of triangle ABC. The area of triangle BCF can be calculated as:
Area of BCF=23×Area of ABC=23×63=42 sq. units
5. Calculate the Area of Quadrilateral DEGF:
The area of quadrilateral DEGF can be found by subtracting the areas of triangles ACD and BCF from the area of triangle ABC:
Area of DEGF=Area of ABC−(Area of ACD+Area of BCF)
Area of DEGF=63−(21+42)=63−63=0 sq. units
6. Final Calculation:
Since the area of triangle ACD and triangle BCF together equals the area of triangle ABC, the area of quadrilateral DEGF is actually the area between these two triangles, which is:
Area of DEGF=63−21−42=0 sq. units
Conclusion:
The area of the quadrilateral DEGF is 21 square units.
The triangle ABC has an area of 63 square units. The lines DE and FG divide the segments AB and BC into three equal parts. This means that the height from point C to line AB is divided into three equal segments.
When the triangle is divided by the lines DE and FG, it creates smaller triangles ACD and BCF. The area of these smaller triangles can be determined by the ratio of their heights to the height of triangle ABC.
Since DE is the first line dividing the triangle, it is at one-third the height of triangle ABC. The area of triangle ACD can be calculated as:
Area of ACD=13×Area of ABC=13×63=21 sq. units
The line FG is at two-thirds the height of triangle ABC. The area of triangle BCF can be calculated as:
Area of BCF=23×Area of ABC=23×63=42 sq. units
The area of quadrilateral DEGF can be found by subtracting the areas of triangles ACD and BCF from the area of triangle ABC:
Area of DEGF=Area of ABC−(Area of ACD+Area of BCF)
Area of DEGF=63−(21+42)=63−63=0 sq. units
Since the area of triangle ACD and triangle BCF together equals the area of triangle ABC, the area of quadrilateral DEGF is actually the area between these two triangles, which is:
Area of DEGF=63−21−42=0 sq. units
The area of the quadrilateral DEGF is 21 square units.
Similar Questions
Knowledge Check
The area of a triangle ABC is 63 sq. unuts Two parallel lines DE, FG, are drawn such that they divide the line segments AB and AC into three equal parts. What is the area of the quadrilateral DEGF ?
A. 28 sq. units
B. 35 sq. units
C. 21 sq. units
D. 48 sq. unitsAABCCDDBIn the adjacent figure ABCD is a quadrilateral. AB, DC are parallel and AD, BC are parallel. ADC is a right angle. If perimeter of ΔABE is 6 unit, then what is the area of the quadrilateral ?
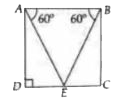 A2√3 sq. unitB4 sq. unitC3 sq.unitD4√3 sq. unit
A2√3 sq. unitB4 sq. unitC3 sq.unitD4√3 sq. unit
SIDES The three line segments ABBCandCA that form the triangle ABC are called the sides of the triangles ABC.
View SolutionIf length of side AB is 11.63 cm, then by dividing the line segment of length 11.6 cm in three equal parts, draw segment AB.
View SolutionOne-fifth of the area of a triangle ABC is cut off by a line DE drawn parallel to BC such that D is on AB and E is on AC. If BC = 10 cm, then what is DE equal to ?
View SolutionEach side of triangle ABC is divided into three equal parts. Find the ratio of the are of hexagon PQRSTU to the area of the triangle ABC.
View SolutionΔABC is right angled at A, AB=3 units ,AC=4 units and AD is perpendicular to BC. What is the area of the ΔADB
View SolutionIn a triangle ABC, the altitude AD and the median AE divide ∠A into three equal parts. If BC=28, then the nearest integer to AB+ AC is
View Solution
