PQ is the perpendicular bisector of AD.AB⊥larBC and DC⊥larBC. If AB=9BC=8 and CD=7. Then the area of quadrilateral APQB.
A
26
B
27
C
25
D
24
Text Solution
The correct Answer is:a
|
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - IV (More than one correct answer Type Questions)
3 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - IV (Matrix Matching Type Questions)
2 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - III (Straight Objective Type Question)
62 Videos
- PLANESBOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
Similar Questions
Knowledge Check
In the given figure, AB⊥AD,BC⊥BD and AD = 9 cm, BC = 8 cm and CD= 17 cm. Find the area of quadrilateral ABCD
 A112 cm2B114 cm2C119 cm2D117 cm2
A112 cm2B114 cm2C119 cm2D117 cm2In a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
A192cm2B232cm2C172cm2Dnone of theseABCD is a trapezium such that AB and CD are parallel and BC⊥CD if ∠ADB=θ,Bc=pandCD=q, then AB is equal to
A(p2+q2sinθpcosθ+qsinθB(p2+q2)cosθpcosθ+qsinthetCp2+q2p2cosθ+q2sinθD(p2+q2)sinθ(pcosθ+qsinθ)
ABCD is a trapezium such that AB and CD are parallel and BC⊥CD. If ∠ADB=θ,BC=pandCD=q, then AB is equal to
View SolutionIn a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
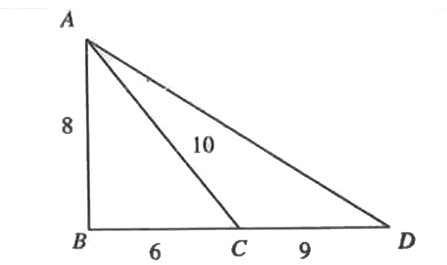
View SolutionIn the figure, if AB=8,BC=6,AC=10andCD=9, then AD =
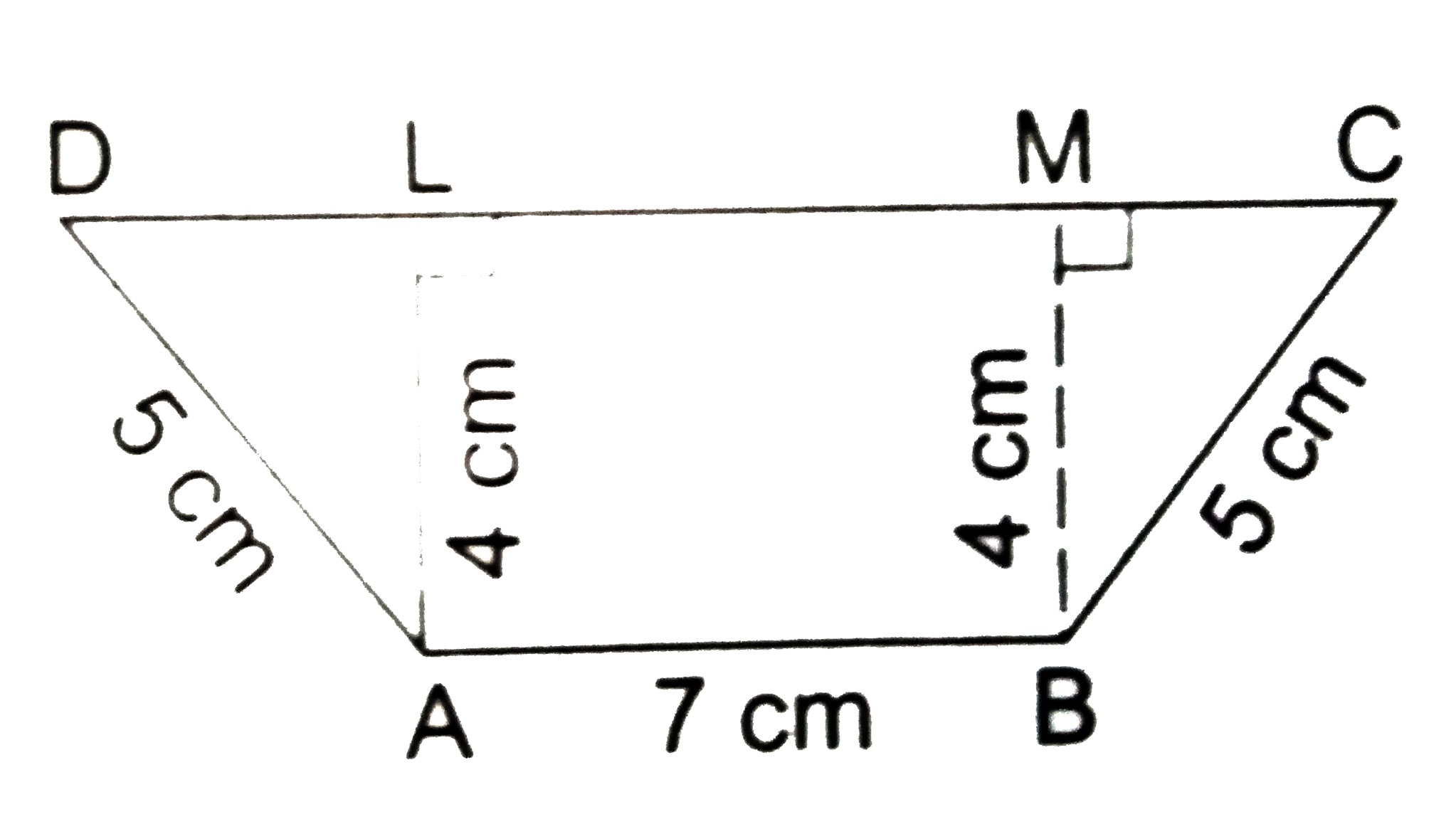
View SolutionIn the given figure, ABCD is a trapezium such that AL⊥DCandBM⊥DC. If AB=7cm,BC=AD=5cm and AL=BM=4cm then ar(trap.ABCD)=?
View SolutionIn ΔABC,∠C=90∘. D is the midpoint BC : and DE⊥AB at E. If AB =13 cm and BE =5 cm, then the area of the square drawn on BC is equal to :
View Solution
