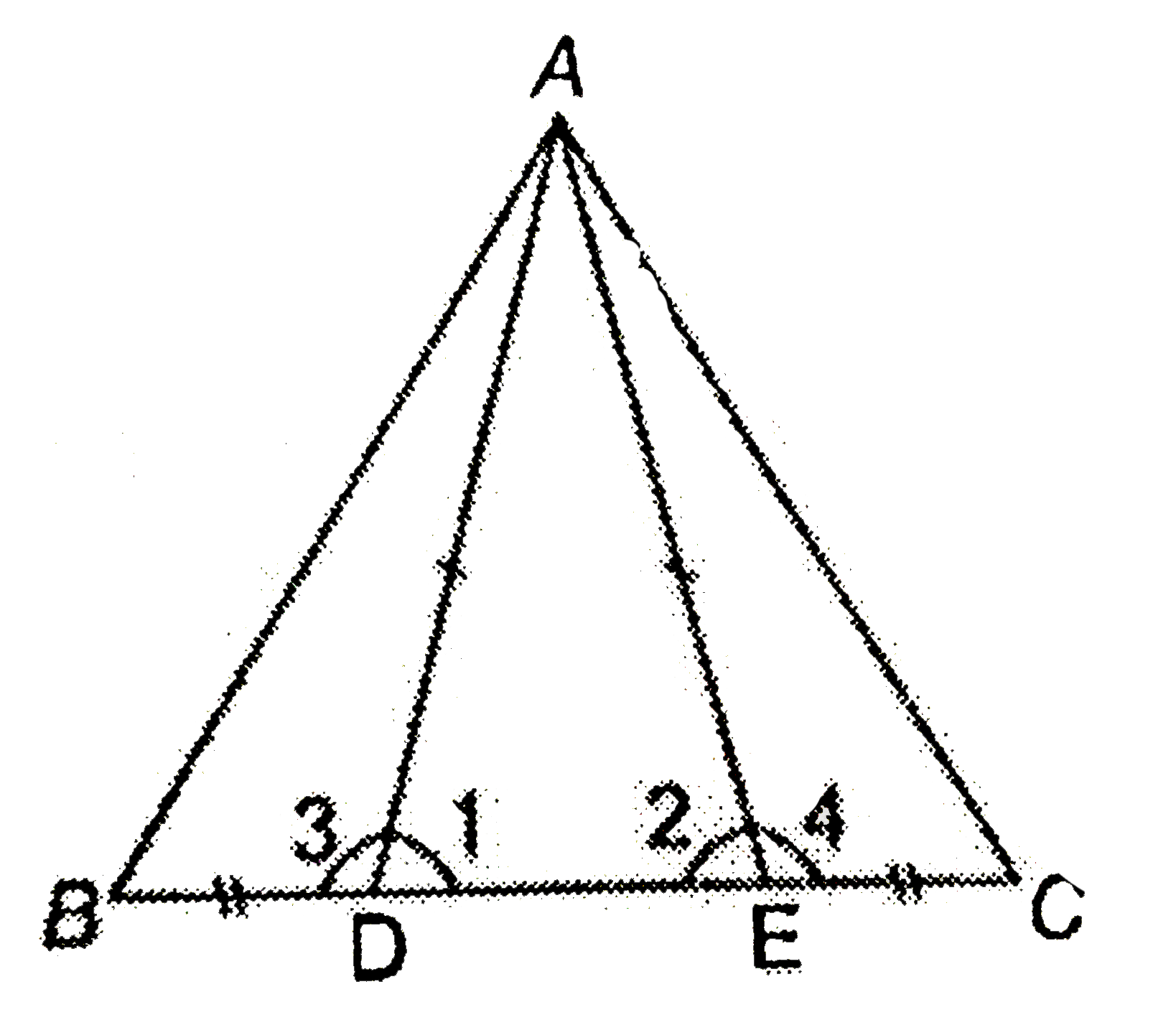
In ΔABC. on the side BC, D and E are two points such that BD=DE=EC. Also ∠ADE=∠AED=α
3(atanB+tanC)=2tanalph
tanB+tanC=3tanα
tanA=6tanαtan2α−9
A=6tanαtan2α−9
The correct Answer is:ad
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - IV (More than one correct answer Type Questions)
3 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - IV (Matrix Matching Type Questions)
2 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - III (Straight Objective Type Question)
62 Videos
- PLANESBOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
Similar Questions
In a triangle ABC, points D and E are taken on side BC such that BD= DE= EC. If angle ADE = angle AED = θ, then: (A) tan θ= 3 tan B (B) 3 tan θ = tan C
View SolutionIn a triangle ABC, points D and E are taken on side BC such that BD= DE= EC. If angle ADE = angle AED = θ, then: (A) tan θ= 3 tan B (B) 3 tan θ = tan C
View Solution
Knowledge Check
In a ΔABC,D and E are two points on AC & BC such that DE is prependicular to BC. DE=18 cm , CE=5cm&tan(∠ABC)=3.6. Find the ratio AC to CD.
ABC2CEB2BCCECCE2BCD∘CEBC
In a triangle ABC, points D and E are taken on side BC such that BD= DE= EC. If angle ADE = angle AED = θ, then: (A) tan θ= 3 tan B (B) 3 tan θ = tan C (C) (6tan θ)/(tan2 θ-9)= tanA (D) ∠B=∠C
View SolutionPoint D,E are taken on the side BC of an acute angled triangle ABC,, such that BD=DE=EC. If ∠BAD=x,∠DAE=yand∠EAC=z then the value of sin(x+y)sin(y+z)sinxsinz is ______
View SolutionPoint D,E are taken on the side BC of an acute angled triangle ABC,, such that BD=DE=EC. If ∠BAD=x,∠DAE=yand∠EAC=z then the value of sin(x+y)sin(y+z)sinxsinz is ______
View SolutionIn Fig. 30 D and E are to points on BC such that BD=DE=EC. Show that ar(ABD)=ar(ADE)=ar(AEC).
View SolutionIn a Δ ABC , D and E are two points on BC such that BD : DE : EC = 4 : 5 : 6 If the area of ΔADE=30cm2. find area of ΔABC
View SolutionIn a triangle ABC, if a=5,b=4andc=3,DandE are the points on BC such that BD=DE=EC. If ΔDAE=θ, then tanθ=
View SolutionIn the given figure, D and E are the points on the base BC of ΔABC such that BD=CE,AD=AE and ∠ADE=∠AED, prove that ΔADB≅ΔAEC.
View Solution
