Let O be the circumcentre, H be the orthocentre, I be the incentre and I1I2,I3 be the excentres of acuteangled ΔABC
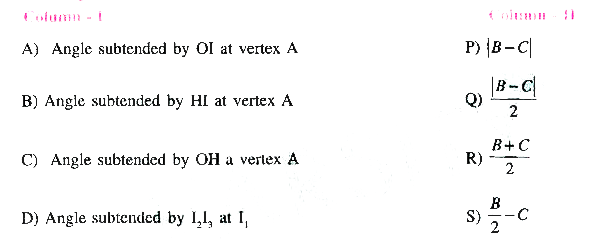
The correct Answer is:A, B, C, D
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL 1 (MAIN)) (Straight Objective Type Questions)
59 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL II) (LECTURE SHEET (ADVANCED)) (More than one correct answer Type Questions)
19 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - PRACTICE SHEET (EXERCISE-IV) (LEVEL-II) (Straight Objective Type Questions)
11 Videos
- PLANESBOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
Similar Questions
Let O be the circumcenter, H be the orthocenter, I be the incenter, and I1,I2,I3 be the excenters of acute-angled ΔABC

View SolutionLet O be the circumcenter, H be the orthocentre, I be the incenter, and I1,I2,I3 be the excenters of acute-angled ABC. Column I Column II Angle subtended by OI at vertex A p. |B−C| Angle subtended by HI at vertex A q. ∣∣∣B−C2∣∣∣ Angle subtended by OH at vertex A r. B+C2 Angle subtended by I2I3atI1 A q. B2−C
View Solution
Knowledge Check
ABC is a triangle whose circumcentre, incentre and orthocentre are O, I and H respectively which lie inside the triangle, then :
A∠BOC=AB∠BIC=π2+A2C∠BHC=π−AD∠BHC=π−A2
Let S be the circumcentre and I be the incentre of acute angled ∠ABC then the angle subtended by SI at vertex A is
View SolutionThe triangle formed by joining the three excentres I1,I2andI3, of ΔABC is called the excentral orexcentric triangle and in this case internal angle bisector of triangle ABC are the altitudes of triangles I1I2I3 Incentre I of ΔABC is the ......... of the excentral ΔI1I2I3.
View SolutionIf is the incentre of ΔABCandI1, is the excentre opposite to the vertex. 'A' of ΔABC, thern II1=
View SolutionABC is a triangle whose circumcentre, incentre and orthocentre are O, I and H respectively which lie inside the triangle, then :
View SolutionVertex A of a variable triangle ABC, inscribed in a circle of radius R, is a fixed point. If the angles subtended by the side BC at orthocentre (H), circumcentre (O) and incentre (I) are equal than identify the locus of orthocentre of triangle ABC.
View SolutionO,G,I and H are respectively the circumcentre, centroid, incentre and orthocentre of an equilateral triangle. Which of these points are identical ?
/ O, G, I तथा H क्रमशः एक समबाह त्रिभुज के परिकेंद्र, केंद्रक, अंतःकेंद्र और लम्बकेंद्र हैं | निम्न में से कौन से बिंदु समसरूप हैं ?
View SolutionO, G, I and H are respectively the circumcenter, centroid, incentre and orthocentre of an equilateral triangle. which of these points are identical?
किसी समबाहु त्रिभज में O, G, I और H क्रमशः परिकेद्र(circumcentre), केंद्रिका (centroid),अंत:केंद्र(incentre)और लंबकेंद्र (orthocentre) है| इनमें से कौन से बिंदु एक समान हैं?
View Solution
