In acute-angled $Δ A B C, a > b > c$ ,
Statement-1: $r_{1} > r_{2} > r_{3}$
Statement-2: $cos A < cos B < cos C$ Solution in Telugu

Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1

Statement-1 is True, Statement-2 is True, Statement-2 NOT a correct explanation for Statement-1

Statement-1 is True, Statement-2 is False

Statement -1 is False, Statement-2 is True

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for In acute-angled DeltaABC, a gt b gt c, Statement-1: r_(1) gt r_(2) gt r_(3) Statement-2: cosA lt cosB lt cosC by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS SOLUTIONS AND PROPERTIES OF TRIANGLES

Topper's Solved these Questions

BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL II) (LECTURE SHEET (ADVANCED)) (More than one correct answer Type Questions)
19videos
PROPERTIES OF TRIANGLES
BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL II) (LECTURE SHEET (ADVANCED)) (Matrix Matching Type Questions)
9videos
PROPERTIES OF TRIANGLES
BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - PRACTICE SHEET (EXERCISE-IV) (LEVEL-II) (Matrix Matching Type Questions)
2videos
PROPERTIES OF TRIANGLES
BOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30videos
PLANES
BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55videos
PROPERTIES OF VECTORS

Similar Questions

In a triangle ABC, the altitude from A is not less than BC and the altitude from B is not then less than AC. The triangle is
05:13
View Solution
Observe the following Columns.

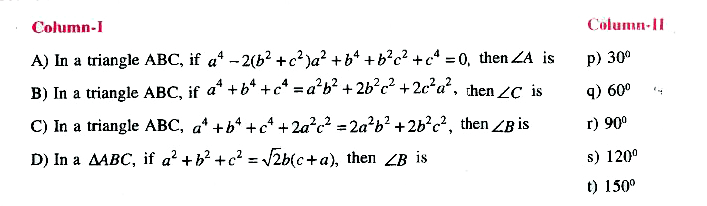05:16
View Solution
Let O be the circumcentre, H be the orthocentre, I be the incentre and $I_{1} I_{2}, I_{3}$ be the excentres of acuteangled $Δ A B C$

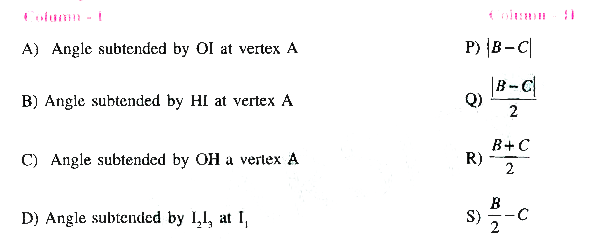View Solution
The plane 2x + 3y + kz - 7 = 0 is parallel to the line whose d.r's are (2,-3,1) then k=
01:33
View Solution
If $¯ ¯¯¯¯ ¯ O A = ¯ i + 2 ¯ j - 3 ¯ k, ¯ ¯¯¯¯ ¯ O B = 3 ¯ i - 2 ¯ j + 5 ¯ k and 2 ¯ ¯¯¯¯ ¯ A C = 3 ¯ ¯¯¯¯ ¯ A B then ¯ ¯¯¯¯ ¯ A C =$
View Solution
The magnitude of gratitational field intensities at distance r_(1) and r_(2) from the centre of a uniform solid sphere of radius R and mass M are I_(1) and I_(2) respectively. Find the ratio of I_(1)//I_(2) if (a) r_(1) gt R and r_(2) gt R and (b) r_(1) lt R and r_(2) lt R (c ) r_(1) gt R and r_(2) lt R .
01:40
View Solution
In an acute angled triangle ABC, $r + r_{1} = r_{2} + r_{3} and ∠ B > \frac{π}{3}$ , then
04:20
View Solution
Statement I In a $Δ A B C, if a < b < c$ and ri si inradius and $r_{1}, r_{2} + r_{2} r_{3}$ are the exradii opposite to angle A,B,C respectively, then $r < r_{1} < r_{2} < r_{3} .$
Statement II For, $Δ A B C r_{1} r_{2} + r_{2} r_{3} + r_{3} r_{1} = \frac{r_{1} r_{2} r_{3}}{r}$
View Solution
In a triangle, if $r_{1} > r_{2} > r_{3},$ then show $a > b > c .$
View Solution
Statement 1: in a $Δ A B C$ if $a < b < c$ and r inradius and $r_{1}, r_{2}, r_{3}$ are the exradii opposite to angle $r > r_{1} > r_{2} > r_{3}$ respectively then
Statement 2: For , $Δ A B C r_{1} r_{2} + r_{2} r_{3} + r_{3} r_{1} = \frac{r_{1} r_{2} r_{3}}{r}$
View Solution
In a triangle with sides $a, b, c, r_{1} > r_{2} > r_{3}$ (which are extradii), then
02:07
View Solution
In an acute angled triangle ABC, $r + r_{1} = r_{2} + r_{3} and ∠ B > \frac{π}{3}$ , then
03:13
View Solution
The magnitudes of the gravitational fields at distances $r_{1}$ and $r_{2}$ from the centre of a uniform sphere of radius R and mass M are $F_{1}$ and $F_{2}$ respectively then
(a) $\frac{F_{1}}{F_{2}} = \frac{r_{1}}{r_{2}}$ if $r_{1} < R$ and $r_{2} < R$
(b) $\frac{F_{1}}{F_{2}} = {(\frac{r_{2}}{r_{1}})}^{2}$ if $r_{1} > R$ and $r_{2} > R$
(c) $\frac{F_{1}}{F_{2}} = \frac{r_{1}}{r_{2}}$ if $r_{1} > R$ and $r_{2} > R$
(d) $\frac{F_{1}}{F_{2}} = {(\frac{r_{1}}{r_{2}})}^{2}$ if $r_{1} < R$ and $r_{2} < R$
06:00
View Solution
The magnitudes of the gravitational fields at distances $r_{1}$ and $r_{2}$ from the centre of a uniform sphere of radius R and mass M are $F_{1}$ and $F_{2}$ respectively then
(a) $\frac{F_{1}}{F_{2}} = \frac{r_{1}}{r_{2}}$ if $r_{1} < R$ and $r_{2} < R$
(b) $\frac{F_{1}}{F_{2}} = {(\frac{r_{2}}{r_{1}})}^{2}$ if $r_{1} > R$ and $r_{2} > R$
(c) $\frac{F_{1}}{F_{2}} = \frac{r_{1}}{r_{2}}$ if $r_{1} > R$ and $r_{2} > R$
(d) $\frac{F_{1}}{F_{2}} = {(\frac{r_{1}}{r_{2}})}^{2}$ if $r_{1} < R$ and $r_{2} < R$
05:17
View Solution
The magnitude of gravitational field at distances r_(1) and r_(2) from the center of a uniform sphere of radius R and mass M are respectively I_(1) and I_(2) . The ratio I_(1)//I_(2) is given in the column II. Make correct matching {:("Column-I",,"Column-II"),((A) r_(1) gt R and r_(2) gt R,,(P) (r_(1)r_(2)^(2))/(R_(3))),((B) r_(1) lt R and r_(2) gt R,,(Q) (R_(3))/(r_(2)r_(1)^(2))),((C) r_(1) gt R and r_(2) lt R,,(R) (r_(1))/(r_(2))),((D) r_(1) lt R and r_(2) gt R,,(S)(r_(2)^(2))/(r_(1)^(2))):}
01:54
View Solution

AAKASH SERIES-PROPERTIES OF TRIANGLES-ADDITIONAL PRACTICE EXERCISE (LEVEL 1 (MAIN)) (Straight Objective Type Questions)

If H is the orthocentre of a acute-angled triangle ABC whose circumcir...
04:12
In triangle ABC, line joining the circumcenter and orthocenter is para...
04:22
A variable triangle ABC is circumscribed about a fixed circle of unit ...
Text Solution
In triangle ABC, angleA=60^(@), angle B=40^(@), and angle C=80^(@) If ...
05:05
In DeltaABC with fixed length of BC, the internal bisector of angle C ...
04:28
The ratio of the area of a regular polygon of n sides inscribed in a c...
03:23
In acute-angled DeltaABC, a gt b gt c, Statement-1: r(1) gt r(2) gt ...
01:42
Statement 1: If the quadrilateral Q(1) formed by joining midpoints of...
06:29
Suppose a, b, g and d are the interior angles of regular pentagon, he...
06:25
In a DeltaABC,b=12 units, c=5 units and Delta=30 sq.units. If d is the...
Text Solution
The length of the tangents drawn from the vertices A, B, and C to the ...
Text Solution
Points D,E are taken on the side BC of a triangle ABC, such that BD=DE...
05:25
Three circles touch one another externally , The tangents at their poi...
04:23
In DeltaAEX, T is the midpoint of XE, and P is the midpoint of ET. If ...
Text Solution
In triangle ABC. Dis on AC such that AD = BC, BD = DC, angleDBC = 2the...
06:17
A triangle has sides 6,7 and 8. The line through its incentre parallel...
03:27
In a triangle ABC if cosAcosB+sinAsin BsinC= then a : b: c=
04:39
In a triangle ABC, D, E are two points on the side BC such that BD = D...
Text Solution
If a = 18, b=24, c= 30 and if l = r2- r1 , m = r3 - r2 , n= r3 - r1 ...
05:38
Delta^("le")ABC is right angled at A the point P and Q are on the hypo...
08:46

Home
Ask Doubt
Profile

In acute-angled ΔABC,a>b>c, Statement-1: r1>r2>r3 Statement-2: cosA<cosB<cosC Solution in Telugu

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

AAKASH SERIES-PROPERTIES OF TRIANGLES-ADDITIONAL PRACTICE EXERCISE (LEVEL 1 (MAIN)) (Straight Objective Type Questions)

In acute-angled $Δ A B C, a > b > c$ ,
Statement-1: $r_{1} > r_{2} > r_{3}$
Statement-2: $cos A < cos B < cos C$ Solution in Telugu