Derive the expression for emf induced in a straight conductor moving perpendicular to a uniform magnetic field.Solution in Kannada
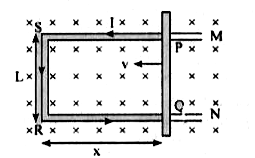
Consider metallic frame MSRN placed in a uniform constant magnetic field. Let the magnetic field B be perpendicualr to the plane of the coil. Let a metal rod PQ of length .l. placed on it be moving towards left with a velocity v as shown in the figure. Let the distance of PQ from SR be x
The magnetic flux linked with the area SPQR is
ϕB=BAcosθ
=Blxcos0=Blx
As the rod PQ is moving towards left with a velocity v, x is changing and
→v=−dxdt ___(1)
Hence Induced emf ε=−dϕBdt=−d(Blx)dt=−Bldxdt
⇒ε=Blv (∵ eqn (1))
This emf is induced in the rod because of the motion of the rod in the magnetic field. Therefore this emf is called motional emf.
Topper's Solved these Questions
- BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014EXERCISE - PART-D (IV. Answer any two of the following questions.)3videos
SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014
- BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014EXERCISE - PART-D (V. Answer any two of the following.)3videos
SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014
- BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014EXERCISE - PART-B (II. Answer any five of the following questions.)8videos
SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014
- BOOK - SUNSTAR PUBLICATIONCHAPTER - P.U. BOARD LATEST MODEL QUESTION PAPER-3EXERCISE - PART-D11videos
P.U. BOARD LATEST MODEL QUESTION PAPER-3
- BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JULY -2015EXERCISE - PART-D11videos
SUPPLEMENTARY EXAM QUESTION PAPER JULY -2015
Similar Questions
Write the expression for electric field intensity at any point outside and inside due to a charged spherical shell.
02:42View SolutionObtain an expression for the total energy of an electron in the nth orbit of hydrogen atom in terms of absolute constants.
01:44View SolutionDerive a relation between electric field and potential
03:28View SolutionWrite the expression for electric field intensity at any point outside and inside due to a charged spherical shell.
01:28View SolutionDerive an expression for the electric field at a point due to an infinitely long thin charged straight wire using Gauss Law.
07:27View SolutionA straight wire of length L is bent into a semicircle. It is moved in a uniform magnetic field with speed v with diameter perpendicular to the field. The induced emf between the ends of the wire is
02:10View SolutionA conductor PQ , with PQ=r , moves with a velocity v in a uniform magnetic field of induced B . The emf induced in the rod is
03:11View SolutionA straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15ms−1 and is directed perpendicular to the field. The emf induced between the two ends of the conductor is
06:10View SolutionObtain an expression for the emf induced across a conductor which is moved in a uniform magnetic field which is perpendicular to the plane of motion.
03:59View SolutionIf a straight conductor moves in a magnetic field, what will be the expression for emf induced in that conductor? On what factors does this emf depend?
06:10View SolutionThe induced emf between the two ends of a straight conductor moving perpendicular to its axis in a uniform magnetic field is
View SolutionA straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15 m/s and is directed perpendicular to the field. The emf induced between the two ends of the conductor is
06:10View SolutionDerive the expression for emf induced in a straight conductor moving perpendicular to a uniform magnetic field.
06:10View SolutionDerive the expression for motional emf induced in a conductor moving in a uniform magnetic field.
04:19View SolutionDerive the expression for emf induced in a straight conductor moving perpendicular to a uniform magnetic field.
02:54View SolutionDerive an expression for the induced emf and induced current produced by changing the area of a rectangular coil placed perpendicular to a uniform magnetic field.
02:43View Solution

