Two girls A nad B run on a circular track with constant speeds such that the ratio of their speeds is 3:5 find the maximum number of distinct points where they can meet if they run the opposite directions.
To solve the problem, we need to find the maximum number of distinct points where two girls A and B can meet while running in opposite directions on a circular track. Given that the ratio of their speeds is 3:5, we can follow these steps:
1. Understanding the Speed Ratio:
- Let the speed of girl A be 3x and the speed of girl B be 5x, where x is a common factor.
2. Calculating Relative Speed:
- Since they are running in opposite directions, their relative speed is the sum of their speeds:
Relative Speed=VA+VB=3x+5x=8x
3. Understanding the Circular Track:
- On a circular track, the maximum number of distinct meeting points is determined by how many times they can meet as they complete laps around the track.
4. Finding the Number of Distinct Meeting Points:
- The maximum number of distinct points where they can meet is equal to the sum of the speeds (in terms of the ratio):
Maximum Distinct Points=Speed of A+Speed of B=3+5=8
5. Conclusion:
- Therefore, the maximum number of distinct points where girls A and B can meet on the circular track is 8.
- Let the speed of girl A be 3x and the speed of girl B be 5x, where x is a common factor.
- Since they are running in opposite directions, their relative speed is the sum of their speeds:
Relative Speed=VA+VB=3x+5x=8x
- On a circular track, the maximum number of distinct meeting points is determined by how many times they can meet as they complete laps around the track.
- The maximum number of distinct points where they can meet is equal to the sum of the speeds (in terms of the ratio):
Maximum Distinct Points=Speed of A+Speed of B=3+5=8
- Therefore, the maximum number of distinct points where girls A and B can meet on the circular track is 8.
Topper's Solved these Questions
Similar Questions
Two girls A and B runs on a circular tracks with the speed of 80 m/s and 140 m/s find the maximum number of distinct points where they can meet if they run in the opposite direction.
View SolutionTwo girls A and B runs on a circular tracks with the speed of 80 m/s and 140 m/s find the maximum number of distinct points where they can meet if they run in the same direction.
View Solution
Knowledge Check
A car runs on a circular track at a constant speed. The circular track has a radius of 100m. If the car takes 62.8 on each lap, its average speed is
A20ms−1B10ms−1C5ms−1DzeroAkbar, Birbal and Chanakya run around a circular track of length 500 m. Akbar and Birbal run with the speeds of 15 m/s and 20 m/s in the same direction respectively and Chanakya being very intelligent run in the opposite direction with a speed of 25 m/s. If all three of them start at the same time, then :
AAkbar meets Chanakya more frequently than Birbal doesBAkbar and Chanakya meets as frequently as Birbal and ChanakyaCAkbar meets Birbal least frequentlyDNothing can be concludedAkbar, Birbal and Chanakya run around a circular track of length 500 m. Akbar and Birbal run with the speeds of 15 m/s and 20 m/s in the same direction respectively and Chanakya being very intelligent run in the opposite direction with a speed of 25 m/s. If all three of them start at the same time, then :
AAkbar meets Chanakya more frequently than Birbal doesBAkbar and Chanakya meets as frequently as Birbal and ChanakyaCAkbar meets Birbal least frequentlyDNothing can be concluded
Two hands of a normal clock run at the speed of 30∘ per hour and 360∘ per hour find the number of distinct points where they meet on the dail.
View SolutionA ,B and C run on a circular track of 800 m speeds of A,B and C are 20 m/s ,26 m/s and 33 m/s what is the ratio of distance covered by each one to meet for the first time?
View SolutionAn athlete runs on a circular track, whose radius is 50 m with a constant speed. It takes 50 seconds to reach point B from starting point A . Find
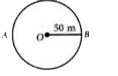
the speed
View SolutionAn athlete runs on a circular track, whose radius is 50 m with a constant speed. It takes 50 seconds to reach point B from starting point A . Find

the displacement
View SolutionAn athlete runs on a circular track, whose radius is 50 m with a constant speed. It takes 50 seconds to reach point B from starting point A . Find
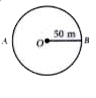
the distance covered
View Solution
