A large vessel is filled with a liquid. Two vertical plates touch the surlace of the liquid (Fig. 25.7). The dimensions of the plates are a and b, the distance between them is d. The plates have been charged by applying a voltage Po and then disconnected from the voltage source. To what height will the liquid rise? Ignore capillary effects.
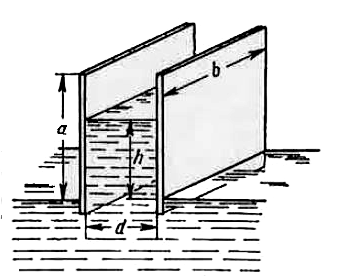
When the liquid flows through a strongly non-uniform electric field close to the edges of the plates, it is polarized and drawn into the space between the plates. Since the charge on the plates remains unchanged in the process, and the capacitance of the capacitor increases, this is accompanied by a decrease in the energy of the field. This decrease is compensated by the increase in the potential energy of the column of líquid held between the plates. From the law of conservation of energy
q22C0=q22C+mgh2
Here C0=ε0abd,C=ε0bd[a+(ε−1)h] (see Problem 25.5) m=ρbhd. Substituting these values into the first formula we obtain, after some simplifications,
(ε−1)q2=ε0ρgab2[a+(ε−1)h]
Express the charge on the plates in terms of the potential,
q=φ0C0=ε0φ0ab/d
After simplifications we obtain a quadratic equation
h2+aε−1h−ε0aφ20ρgd2=0
Solving it we obtain the height the liquid rises.
समान प्रश्न
कांच की दो समांतर प्लेटों ρ घनत्व वाले द्रव में लम्बवत डुबोया जाता है। प्लेटों के बीच की दूरी d व द्रव का पृष्ठ तनाव T है। कांच का स्पर्श कोण θ है तो दोनों प्लेटों के द्रव का केशिका उन्नयन होगा
View SolutionTwo parallel glass plates are dipped perpendiculary in a liquid of density p. The separation between the plates is 'd' and the surface tension T. The angle of contact of glass is θ. The capillary rise of the liquid between the plates is
View SolutionTwo parallel glass plates are dipped perpendicularly in a liquid of density ρ. The separation between the plates is ‘d' and the surface tension T. The angle of contact of glass is θ. The capillary rise of the liquid between the plates is
View SolutionTwo parallel glass plates are dipped perpendiculary in a liquid of density p. The separation between the plates is 'd' and the surface tension T. The angle of contact of glass is θ. The capillary rise of the liquid between the plates is
View SolutionTwo parallel glass plates are dipped perpendicularly in a liquid of density rho . The separation between the plates is ‘d' and the surface tension T. The angle of contact of glass is theta . The capillary rise of the liquid between the plates is
View SolutionTwo parallel glass plates are dipped partly in the liquid of density 'd' keeping them vertical. If the distance between the plates is 'x', Surface tension is T and angle of contact is theta then rise of liquid between the plates due to capillary will be
View SolutionWhat is the height to which a liquid rises between two long parallel plates, a distance d apart ? (Surface tension of liquid is T and density is rho )
View Solution
