Determine the load resistance for which the power delivered to the circuit is a maximum. Graph the dependence of the power on the load resistance.
The power Rtot=ε2/(R+r) is at its maximum in conditions of short-circuit (R =0). The short circuit power is Rsh.e=ε2/r.
The power in the external circuil is at its maximum when R = r.
To check this consider the extremum of the expression Pex=ε2r.Rr(R+r)2=ε2ry
We have
y=(R+r)2Rr=Rr+2+rR=Rr−2+rR+r=
=(√Rr−√rR)2+4
Obviously, y= 4 for R = r is minimum value. In this case the power in the external circuit is maximum. The corresponding graphs are shown in Fig. 26.13. 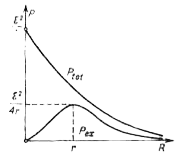
Similar Questions
In a common emitter amplifier , the load resistance of the output circuit is 500 times the resistance of the input circuit. If α=0.98 , then find the voltage gain and power gain .
View SolutionA power supply with an e.m.f epsi and internal resustance r is connected to a variable resistance R. Find the dependence of the total power generated by the supply and of the power delivered to the external circuit on the load resistance.
View SolutionA power supply with an e.m.f epsi and internal resustance r is connected to a variable resistance R. Find the dependence of the total power generated by the supply and of the power delivered to the external circuit on the load resistance.
View SolutionDetermine the load resistance for which the power delivered to the circuit is a maximum. Graph the dependence of the power on the load resistance.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionA cell of emf 16V and internal resistant 4Ω can deliver maximum power to a load of resistance R where R is equal to
View SolutionIn the situation shown each cell has e.m.f. 4V and internal resistance 1Ω. The maximum power that can be delivered to the variable load resistance R is

View Solution
