A rod of length l is perpendicular to the lines of induction of a uniform magnetic field of induction B. The rod revolves at an angular speed ω about an axis passing through the rod's end parallel to the lines of induction. Find the voltage across the rod's ends.
The correct Answer is:△Ψ=Bωl2/2.
The rod moves perpendicularly to the lines of induction of the magnetic field, and in a small section of it an elementary e.m.f △ε=Bv△x is established, △x being the length of the section and v Its velocity (see Fig. 30, 4a). The voltage across the rod is the sum of the elementary e.m.f..s. Since v=ωr,△ε=Bωx△x. The result may be found by two methods:
(a) By integration. We have △Ψ=1∫0Bωxdx=Bω[x22]l0=12Bwl2
(b) Graphically. Plot a graph of the strength of the induced field E⋅=△ε/△x=Bωx. Since this is a linear function, its graph is of the form shown in Fig 30.4 b. The voltage is numerically equal to the area under the graph : △Ψ=lBwl2−Bwl22 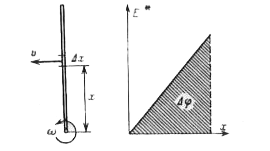
Similar Questions
A rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v_(0) hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.
05:16View Solutionl लम्बाई की एक छड़ को इसके मध्य बिन्दु से गुजरने वाले अक्ष के परितः एकसमान कोणीय वेग ω से घुमाया जाता है किन्तु यह घूर्णन अक्ष के समानान्तर दिशा के साथ प्रेरण B के एकसमान चुम्बकीय क्षेत्र में इसकी लम्बाई के लम्बवत् है। छड़ के दोनों सिरों के बीच प्रेरित वि.वा.बल होगा-
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
04:01View SolutionA copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
02:44View SolutionA rod of length l is rotated about its one end, perpendicular to a magnetic field of induction B What is the e.m.f induced in the rod
03:39View SolutionA rod of length l is perpendicular to the lines of induction of a uniform magnetic field of induction B. The rod revolves at an angular speed omega about an axis passing through the rod's end parallel to the lines of induction. Find the voltage across the rod's ends.
View SolutionA horizontal rod of length 'l' rotates about a vertical axis with a uniform angular velocity 'omega' . A uniform magnetic field of induction B exists parallel to the axis of rotation. The potential different between the ends of the rod is
03:20View Solution
