A rod of length l is perpendicular to the lines of induction of a uniform magnetic field of induction B. The rod revolves at an angular speed ω about an axis passing through the rod's end parallel to the lines of induction. Find the voltage across the rod's ends.
The correct Answer is:△Ψ=Bωl2/2.
The rod moves perpendicularly to the lines of induction of the magnetic field, and in a small section of it an elementary e.m.f △ε=Bv△x is established, △x being the length of the section and v Its velocity (see Fig. 30, 4a). The voltage across the rod is the sum of the elementary e.m.f..s. Since v=ωr,△ε=Bωx△x. The result may be found by two methods:
(a) By integration. We have △Ψ=1∫0Bωxdx=Bω[x22]l0=12Bwl2
(b) Graphically. Plot a graph of the strength of the induced field E⋅=△ε/△x=Bωx. Since this is a linear function, its graph is of the form shown in Fig 30.4 b. The voltage is numerically equal to the area under the graph : △Ψ=lBwl2−Bwl22 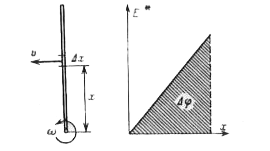
Similar Questions
Moment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View Solution
Knowledge Check
- Question 1 - Select One
Moment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
Aml212Bml23C7ml248Dml29 - Question 2 - Select One
Two balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
A23mωL2B13ω2LmC23ω2LmD13Lm - Question 3 - Select One
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2
Two balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA metallic rod of length lis hinged at one end and the other end is rotated with a constant angular speed ω about an axis passing through the hinge. A constant and uniform magnetic field B, parallel to the axis of rotation exists everywhere. The induced emf between the two ends of rod is 12Blω2.
View SolutionThe radius of gyration of a uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution

