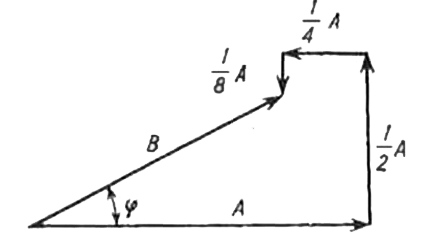
Find the resulting amplitude and phase of the vibrations
s=Acosωt+A2cos(ωt+π2)+A4cos(ωt+π)+A8cos(ωt+3π2)
The correct Answer is:B=3A√58=0.84A;φ=arctan12=0.464 rad =26.6∘
Apply the vector diagram Fig. Here
B=√(A−A4)2+(A1−A8)2,tanφ=(A/4)−(A/8)A−(A/4)=12
Similar Questions
Four simple periodic vibrations y_1=8 cos omegat y_2=4 cos (omegat+pi/2) y_3=2 cos (omegat+pi) y_4=cos (omegat+(3pi)/2) Are implanted with each other, the resulting dimension and art are respectively
View SolutionFour simple harmonic vibrations x1=8sinωt,x2=6sin(ωt+π/2),x3=4sin(ωt+π) and x4=2sin(ωt+3π/2) are superimposed on each other. The resulting amplitude is
View SolutionA vibratory motion is represented by x=2Acosomegat+Acos(omegat+(pi)/(2))+Acos(omegat+pi)+(A)/(2)cos(omegat+(3pi)/(2)) . the resultant amplitude of the motion is
View SolutionWhat is the resulting intensity after interference of two coherent waves given as y_1=a_1 cos omegat and y_2=a_2 cos ((pi)/2-omegat) ?
View SolutionFind the resulting amplitude and phase of the vibrations
s=Acosωt+A2cos(ωt+π2)+A4cos(ωt+π)+A8cos(ωt+3π2)
View SolutionFuncation x=Asin2ωt+Bcos2ωt+Csinωtcosωt Represents SHM.
View Solutionx1=5sin(ωt+30∘)
x2=10cos(ωt)
Find amplitude of resultant SHM.
View Solution
