Radium disintegrates at an average rate of 2.24×1013 α-particles per minute. Each a-particle takes up two electrons from the air and becomes a neutral helium atom. After 420 days, helium gas collected was 0.5 rnL, measured at 27°C and 750 mmHg. Calculate the Avogadro constant.
The correct Answer is:6.7×1023
Topper's Solved these Questions
- ELEMENTARY PROBLEMS BASED ON DEFINITION OF MOLE: THE MOLE CONCEPT BOOK - RC MUKHERJEECHAPTER - ELEMENTARY PROBLEMS BASED ON DEFINITION OF MOLE: THE MOLE CONCEPT EXERCISE - OBJECTIVE PROBLEMS
29 Videos
- ELEMENTARY PROBLEMS BASED ON DEFINITION OF MOLE: THE MOLE CONCEPT BOOK - RC MUKHERJEECHAPTER - ELEMENTARY PROBLEMS BASED ON DEFINITION OF MOLE: THE MOLE CONCEPT EXERCISE - OBJECTIVE PROBLEMS
29 Videos
- ELECTROMOTIVE FORCE BOOK - RC MUKHERJEECHAPTER - ELECTROMOTIVE FORCE EXERCISE - EXERCISE
1 Videos
- EMPIRICAL, MOLECULAR AND STRUCTURAL FORMULAEBOOK - RC MUKHERJEECHAPTER - EMPIRICAL, MOLECULAR AND STRUCTURAL FORMULAEEXERCISE - Problems
46 Videos
Similar Questions
Disintegration of radium takes place at an average rate of 2.24×1013 α-particles per minute. Each α-particle takes up 2 electrons from the air and becomes a neutral helium atom. After 420 days, the He gas collected was 0.5×10−3L measured at 300K and 750mm of mercury pressure. From the above data, calculate Avogadro's number.
View Solution1012α- particles (Nuclei of helium) per second falls on a neutral sphere, calculate time in which sphere gets charged by 2μC.
View Solution
Knowledge Check
Read the following passage carefully and answer the questions
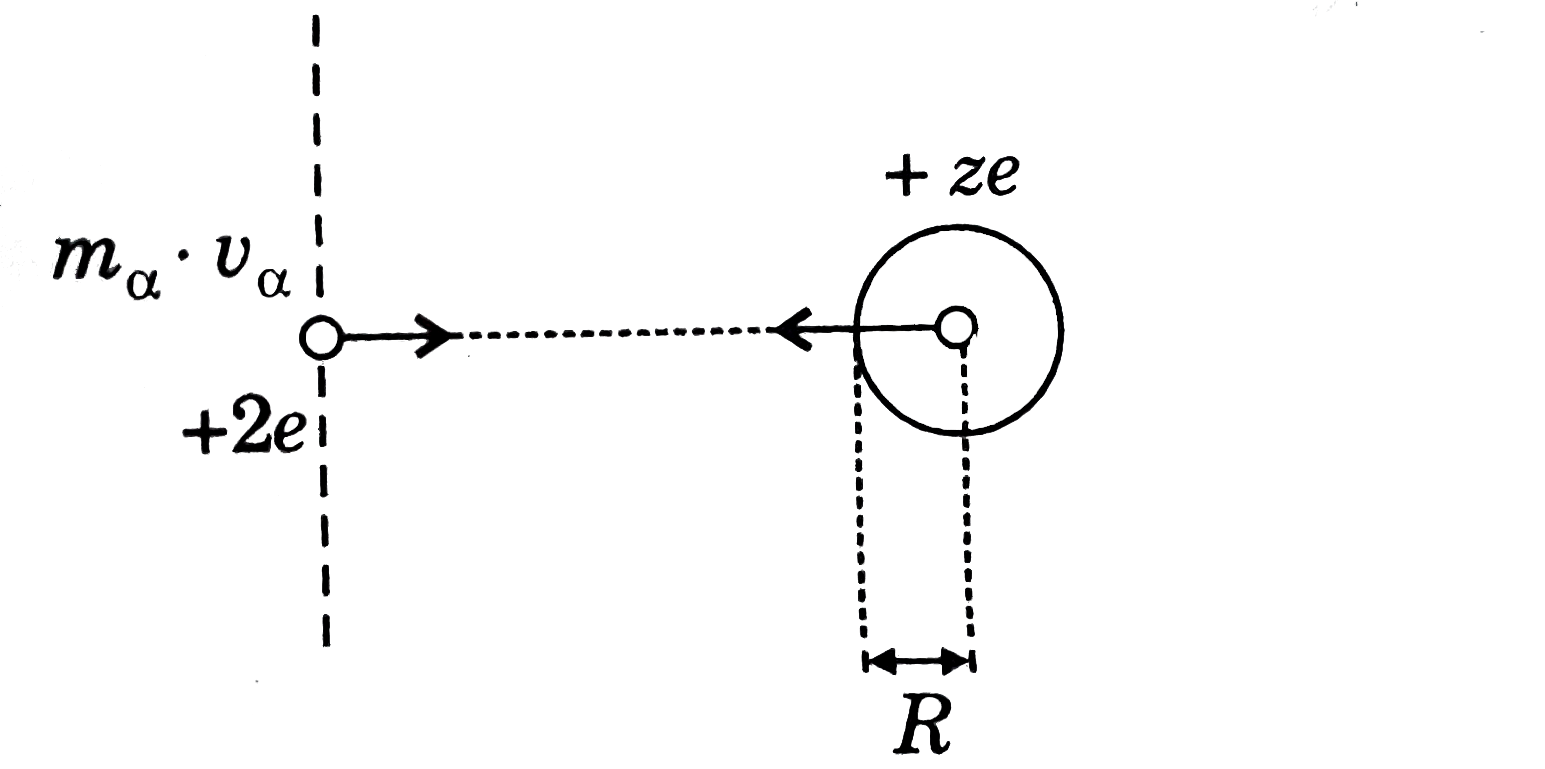
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
Radius of a particular nucleus is calculated by the projection of α−particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , α−particle with half of the earlier speed then the percentage error involved in the radius calculation is :A0.75B1C3D4
1012α- particles (Nuclei of helium) per second falls on a neutral sphere, calculate time in which sphere gets charged by 2μC.
View Solution1012α- particles (Nuclei of helium) per second falls on a neutral sphere, calculate time in which sphere gets charged by 2μC.
View SolutionIn 1908 Rutherford together with H- Geiger measured the rate of emission of α particles (x) by radius (in the nature this element is represented by a single nuclide _(88)226Ra) and found that 1.00g of radius emits x=3.42×1010α- particle per second.
In 1911 Ritherford and American physical chemist B. Boltwood measured the rate of formation of helium from radius. This experiment permits to obtain the most accurate value of Avogadro's number avaliable at the time, given that the value of molar volume of ideal gas was well established. To achieve this goal a sample of radium salt purified from decays products and contaning m=192 mg of Re was put into a device an the volume of the evolved helium was measured. After 83 days (t=83.0days) of the experiment 6.58mm3 of He was collected (VHe=6.58mm3corrected to0∘Cand1atm).
To inderstand the results of this experiment we shall need the kinetic scheme of redioactive decay of Re which is given below (half-lives are the arrows, the type of decay is below the arrows).
Ra>1500years−−−−−−−−−→αRn3.83days−−−−−−−→αRaA3.05min−−−−−−→αRaB26.8−−−−−→βRaC17.7min−−−−−−→β
→RaC'1.63×10−4S−−−−−−−−−→αRaD27.1years−−−−−−−→βRaE5days−−−−−→βPo138days−−−−−−→αPb (stable)
(RaA-RaE are intermediate products of radon decay).
{:a) How many helium atoms were formed each decayed radius atom after 83 days?
{:b) How many helium atom were formed in total during the experiment?
View SolutionIn 1908 Rutherford together with H- Geiger measured the rate of emission of α particles (x) by radius (in the nature this element is represented by a single nuclide .22688Ra) and found that 1.00g of radius emits x=3.42×1010α- particle per second.
In 1911 Ritherford and American physical chemist B. Boltwood measured the rate of formation of helium from radius. This experiment permits to obtain the most accurate value of Avogadro's number avaliable at the time, given that the value of molar volume of ideal gas was well established. To achieve this goal a sample of radium salt purified from decays products and contaning m=192 mg of Re was put into a device an the volume of the evolved helium was measured. After 83 days (t=83.0days) of the experiment 6.58mm3 of He was collected (VHe=6.58mm3corrected to0∘Cand1atm).
To inderstand the results of this experiment we shall need the kinetic scheme of redioactive decay of Re which is given below (half-lives are the arrows, the type of decay is below the arrows).
Ra>1500years−−−−−−−−−→αRn3.83days−−−−−−−→αRaA3.05min−−−−−−→αRaB26.8−−−−−→βRaC17.7min−−−−−−→β
→RaC'1.63×10−4S−−−−−−−−−→αRaD27.1years−−−−−−−→βRaE5days−−−−−→βPo138days−−−−−−→αPb (stable)
(RaA-RaE are intermediate products of radon decay).
Write the first six radioactive dacays using a modern natation showing atomic and mass numbers of all nuclei involved.
As a rough first approximation half-lives of all radius decay products, except those of RaD and Po, may be assumed to be negligible compared to the time of measurement t. Using this approximation perform the following calculations.
View SolutionFive particles are projected simultaneously from the top of a tower that is h=32m high. The initial velocities of projection are as shown in figure. Velocity of 2 and 5 are horizontal.
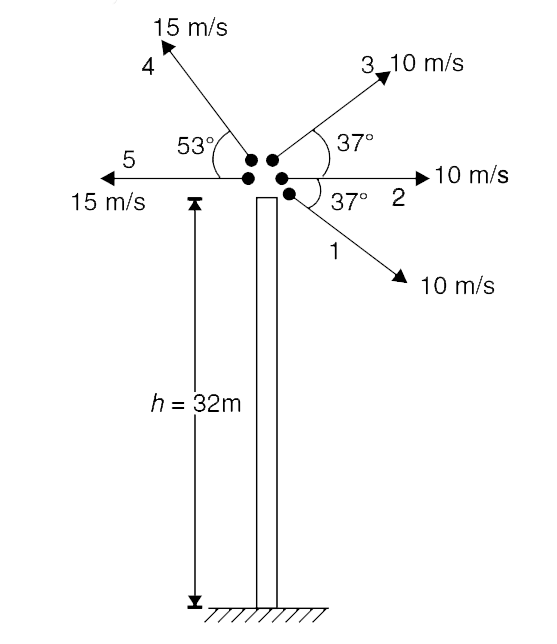
(a) Which particle will hit the ground first?
(b) Separation between which two particles is maximum at the instant the first particle hits the ground?
(c) Which two particles are last and last but one to hit the ground? Calculate the distance between these two particles (still in air), at a time 0.3s after the third particle lands on ground.
[g=10m/s2,tan37∘=34]
View SolutionA radio nuclide consists of two isotopes. One of the isotopes decays by α-emission and other by β-emission with half-lives T1=405s and T2=1620s, respectively. At t=0, probabilities of getting α and β-particles from the radio nuclide are equal . Calculate their respective probabilities at t=1620s. If at t=0, total number of nuclei in the radio nuclide are N0. Calculate the time t when total number of nuclei remained undecayed becomes equal to N0/2.
log102=0.3010, log105.94=0.7742 and x4+4x−2.5=0,x=0.594
View SolutionA radio nuclide consists of two isotopes. One of the isotopes decays by α-emission and other by β-emission with half-lives T1=405s and T2=1620s, respectively. At t=0, probabilities of getting α and β-particles from the radio nuclide are equal . Calculate their respective probabilities at t=1620s. If at t=0, total number of nuclei in the radio nuclide are N0. Calculate the time t when total number of nuclei remained undecayed becomes equal to N0/2.
log102=0.3010, log105.94=0.7742 and x4+4x−2.5=0,x=0.594
View Solution
