1012α- particles (Nuclei of helium) per second falls on a neutral sphere, calculate time in which sphere gets charged by 2μC.
To solve the problem, we need to calculate the time it takes for a neutral sphere to accumulate a charge of 2μC when 1012 alpha particles are falling on it per second.
1. Understanding Alpha Particles:
- An alpha particle is the nucleus of a helium atom, which consists of 2 protons and 2 neutrons.
- The charge of an alpha particle is 2×e, where e is the charge of a proton.
2. Charge of an Alpha Particle:
- The charge of a proton e is approximately 1.6×10−19C.
- Therefore, the charge of an alpha particle is:
q=2×e=2×1.6×10−19C=3.2×10−19C
3. Total Charge Required:
- We need to find the time taken to accumulate a total charge Q of 2μC:
Q=2μC=2×10−6C
4. Number of Alpha Particles per Second:
- The number of alpha particles falling on the sphere per second is given as:
N=1012particles/second
5. Calculating Time:
- The total charge Q accumulated in time T can be expressed as:
Q=N⋅q⋅T
- Rearranging for T:
T=QN⋅q
6. Substituting Values:
- Substitute Q, N, and q into the equation:
T=2×10−6C1012particles/second⋅3.2×10−19C
7. Calculating:
- First, calculate N⋅q:
N⋅q=1012⋅3.2×10−19=3.2×10−7C/second
- Now substitute this back into the equation for T:
T=2×10−63.2×10−7=6.25seconds
Final Answer:
The time taken for the sphere to get charged by 2μC is 6.25 seconds.
- An alpha particle is the nucleus of a helium atom, which consists of 2 protons and 2 neutrons.
- The charge of an alpha particle is 2×e, where e is the charge of a proton.
- The charge of a proton e is approximately 1.6×10−19C.
- Therefore, the charge of an alpha particle is:
q=2×e=2×1.6×10−19C=3.2×10−19C
- We need to find the time taken to accumulate a total charge Q of 2μC:
Q=2μC=2×10−6C
- The number of alpha particles falling on the sphere per second is given as:
N=1012particles/second
- The total charge Q accumulated in time T can be expressed as:
Q=N⋅q⋅T
- Rearranging for T:
T=QN⋅q
- Substitute Q, N, and q into the equation:
T=2×10−6C1012particles/second⋅3.2×10−19C
- First, calculate N⋅q:
N⋅q=1012⋅3.2×10−19=3.2×10−7C/second
- Now substitute this back into the equation for T:
T=2×10−63.2×10−7=6.25seconds
The time taken for the sphere to get charged by 2μC is 6.25 seconds.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-0187videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION9videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
1012α- particles (Nuclei of helium) per second falls on a neutral sphere, calculate time in which sphere gets charged by 2μC.
View SolutionThe atomic weight of radius is 226. It is observed that 3.67×1010 α−particles are emitted per second from one gram of radium. Calculate in years the half period of radium.
View Solution
Knowledge Check
- Question 1 - Select One
A spherical capacitor has an inner sphere of radius 10 cm and outer sphere of radius 12 cm . The outer sphere is earthed and the inner sphere is given a charge of 5μC . The capacitance of the capacitor is
A2.40(πε0)B4.80(πε0)C2.00(πε0)D3.00(πε0) - Question 2 - Select One
The number of α particles emitted per second by 1g of 88226 Ra is 3.7×1010. The decay constant is :
A1.39×10−11sec−1B13.9×10−11sec−1C139×10−10sec−1D13.9×10−10sec−1 - Question 3 - Select One
A conducting sphere carries a net charge of −6μC. The sphere is located at the center of a conducting spherical shell that carries a net charge of +2μC as shown in the figure. Determine the excess charge on the outer surface of the spherical shell.
 A−4μCB+4μCC−8μCD+8μC
A−4μCB+4μCC−8μCD+8μC
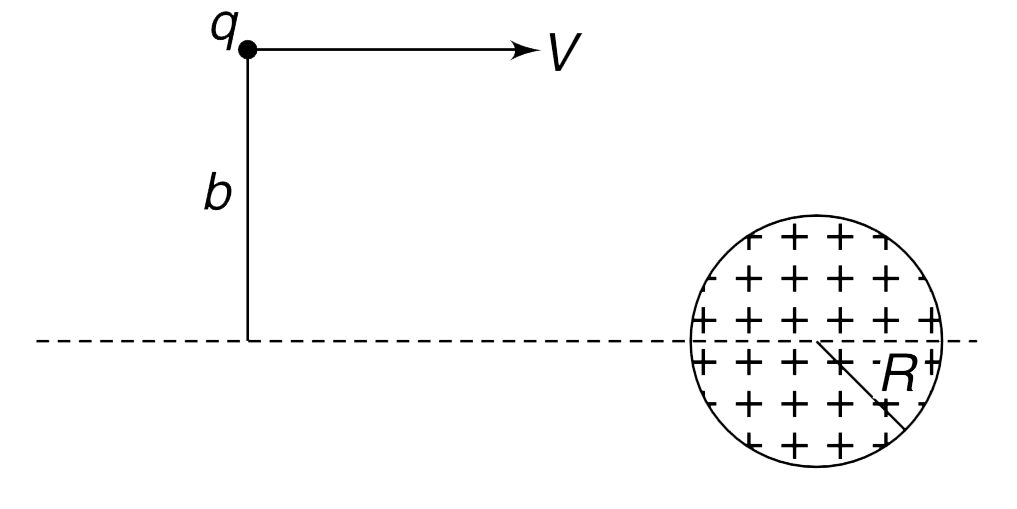
There is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
 View Solution
View SolutionA radioactive source, in the form of a metallic sphere of radius 10−2m emits β−particles at the rate of 5×1010 particles per second. The source is electrically insulated. How long will it take for its potential to be raised by 2V, assuming that 40% of the emitted β−particles escape the source.
View SolutionA spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere si earthed and the inner sphere is given a charge of 2.5μC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor. (b) What is the potential of the inner sphere ?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm.Explain why the latter is much smaller ?View SolutionTwo identical conducting spheres carry charges of +5.0μC and −10μC, respectively. The centers of the spheres are initially separated by a distance L. The two spheres are brought together so that they are in contact. The spheres are then returned to their original separation L. What is the ratio of the magnitude of the electric force on either sphere after the spheres are touched to that before they were touched ?
View SolutionThree metallic spheres A, B and C having radii are in ratio1:2:3. Charge on sphere A is 6 μC and sphere B and C are electrically neutral. If sphere A first contact with sphere B and then from C and ultimately contact from sphere B, then now charge on spheres A, B and C respectively will be-
View Solution

