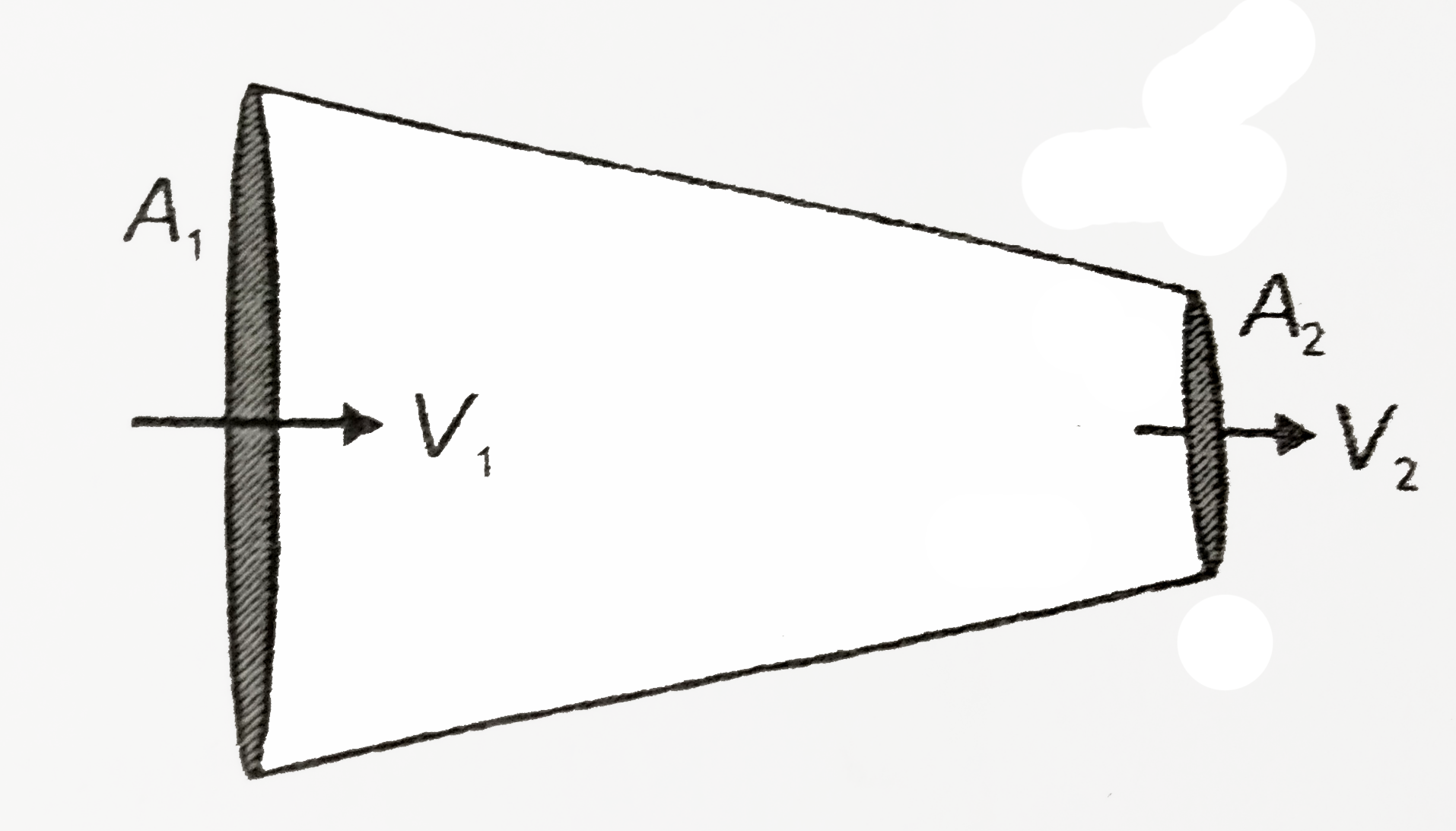
Calculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
To solve the problem of calculating the rate of flow of glycerine through a conical section of a pipe, we can follow these steps:
Step 1: Identify the Given Data
- Density of glycerine, ρ=1.25×103kg/m3
- Radius at one end, r1=0.1m
- Radius at the other end, r2=0.04m
- Pressure drop, ΔP=10N/m2
Step 2: Calculate the Cross-Sectional Areas
Using the formula for the area of a circle, A=πr2:
- Area at the larger end, A1=πr21=π(0.1)2=π(0.01)=0.0314m2
- Area at the smaller end, A2=πr22=π(0.04)2=π(0.0016)=0.005026m2
Step 3: Apply the Continuity Equation
According to the continuity equation:
A1V1=A2V2
From this, we can express the ratio of velocities:
V1V2=A2A1
Substituting the areas:
V1V2=0.0050260.0314≈425
Let’s denote this as Equation (1).
Step 4: Apply Bernoulli's Equation
Using Bernoulli's equation, we have:
P1+12ρV21=P2+12ρV22
Rearranging gives:
12ρV22−12ρV21=P1−P2=ΔP
Substituting ΔP=10N/m2:
12ρ(V22−V21)=10
This simplifies to:
V22−V21=20ρ
Substituting ρ=1.25×103:
V22−V21=201.25×103=0.016m2/s2
Let’s denote this as Equation (2).
Step 5: Substitute Equation (1) into Equation (2)
Using V1=425V2 from Equation (1):
V22−(425V2)2=0.016
This expands to:
V22−16625V22=0.016
Combining terms:
(1−16625)V22=0.016
Calculating the coefficient:
625−16625V22=0.016
609625V22=0.016
Thus:
V22=0.016×625609≈0.0165m2/s2
Calculating V2:
V2≈0.128m/s
Step 6: Calculate the Rate of Flow
The volumetric flow rate Q is given by:
Q=A2V2
Substituting the values:
Q=0.005026×0.128≈6.43×10−4m3/s
Final Answer
The rate of flow of glycerine through the conical section of the pipe is approximately:
Q≈6.43×10−4m3/s
- Density of glycerine, ρ=1.25×103kg/m3
- Radius at one end, r1=0.1m
- Radius at the other end, r2=0.04m
- Pressure drop, ΔP=10N/m2
Using the formula for the area of a circle, A=πr2:
- Area at the larger end, A1=πr21=π(0.1)2=π(0.01)=0.0314m2
- Area at the smaller end, A2=πr22=π(0.04)2=π(0.0016)=0.005026m2
According to the continuity equation:
A1V1=A2V2
From this, we can express the ratio of velocities:
V1V2=A2A1
Substituting the areas:
V1V2=0.0050260.0314≈425
Let’s denote this as Equation (1).
Using Bernoulli's equation, we have:
P1+12ρV21=P2+12ρV22
Rearranging gives:
12ρV22−12ρV21=P1−P2=ΔP
Substituting ΔP=10N/m2:
12ρ(V22−V21)=10
This simplifies to:
V22−V21=20ρ
Substituting ρ=1.25×103:
V22−V21=201.25×103=0.016m2/s2
Let’s denote this as Equation (2).
Using V1=425V2 from Equation (1):
V22−(425V2)2=0.016
This expands to:
V22−16625V22=0.016
Combining terms:
(1−16625)V22=0.016
Calculating the coefficient:
625−16625V22=0.016
609625V22=0.016
Thus:
V22=0.016×625609≈0.0165m2/s2
Calculating V2:
V2≈0.128m/s
The volumetric flow rate Q is given by:
Q=A2V2
Substituting the values:
Q=0.005026×0.128≈6.43×10−4m3/s
The rate of flow of glycerine through the conical section of the pipe is approximately:
Q≈6.43×10−4m3/s
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.19
1 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.20
1 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.17
1 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Calculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
View SolutionThe radii of curvatures of a convex lens are 0.04 m and 0.04m. Its refractive index is 1.5. Its focal length is
View SolutionCalculate the pH of 1.0×103 M solution of NaCI
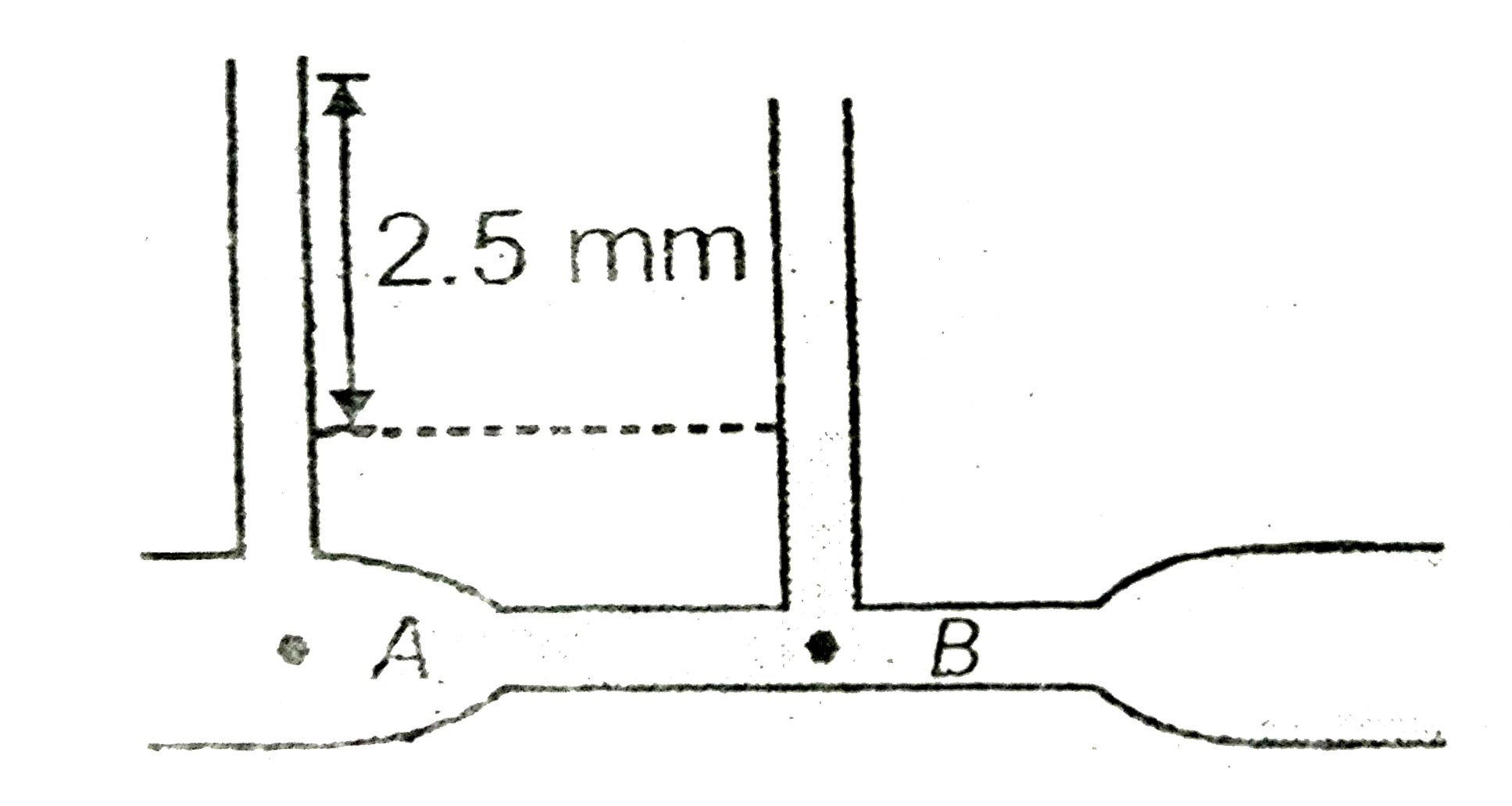
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
View SolutionThe density of iron is 7.8×103kg m−3 What is its relative density?
View SolutionTo what height does a liquid of density 0.4×103 kg m−3 and surface tension 0.05 Nm−1 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cosθ=0.4g=10ms−2]
View SolutionA silver cylindrical rod has a length of 0.5 m and radius of 0.4 m, find the density of the rod, if its mass is 2640 kg.
View SolutionCalculate the speed of a transverse wave in a wire of 1.0mm2 cross-section under a tension of 0.98N. Density of the material of wire is 9.8×103kg/m3
View SolutionThe volume of a cuboid is 7.68m3if its length =3.2 m and height = 1.0 m : find its breadth.
View SolutionTwo metal spheres are falling through a liquid of density 2×103kg/m3 with the same uniform speed. The material density of sphere 1 and sphere 2 are 8×103kg/m3 and 11×103kg/m3 respectively. The ratio of their radii is :-
View Solution
