The CsCl structure is observed in alkali halides only when the radius of the cation is sufficiently large to keep its eight nearest-neighbour anions from touching. What minimum value of r+/r− is needed to prevent this contact?
0.155
0.225
0.414
0.732
The correct Answer is:D
Topper's Solved these Questions
- SOLID AND LIQUID STATES BOOK - RC MUKHERJEECHAPTER - SOLID AND LIQUID STATES EXERCISE - PROBLMES (ANSWERS BRACKTED WITH QUESTIONS)
38 Videos
- PROPERTIES OF GASESBOOK - RC MUKHERJEECHAPTER - PROPERTIES OF GASESEXERCISE - OBJECTIVE PROBLEMS
5 Videos
- VOLUMETRIC CALCULATIONS BOOK - RC MUKHERJEECHAPTER - VOLUMETRIC CALCULATIONS EXERCISE - OBJECTIVE PROBLEMS
37 Videos
Similar Questions
The CsCl type structure is exhibited by alkali halides only when the radius of the cation is large enough to keep touching its eight nearst neighbour aniion. Below what minimum raiton of cation of anion radii (r+/r−) this contact is prevented
View SolutionThe ZnS zinc blende structure is cubic. The unit cell may be described as a face-centered sulfide ion sublattice with zinc ions in the centers of alternating minicubes made by partitioning the main cube into 8 equal parts
(a) How many nearest neighbors does each Zn2+ have ?
(b) How many nearest neighbors does each S2− have?
(c) what angle is made by the line connecting any Zn2+ to any two of its nearest neighbors ?
(d) What minimum r+/r− ratio is needed to avoid anion -anion contact, if closest cation-anion pairs are assumed to touch ?
View Solution
Knowledge Check
The CsCl type structure is exhibited by alkali halides only when the radius of the cation is large enough to keep touching its eight nearst neighbour aniion. Below what minimum raiton of cation of anion radii (r+/r−) this contact is prevented
A0.225B0.414C0.632D0.732The ZnS zinc blende structure is cubic. The unit cell may be described as a face-centered sulfide ion sublattice with zinc ions in the centers of alternating minicubes made by partitioning the main cube into 8 equal parts (as shown in fig)

(a) How many nearest neighbors does each Zn2+ have ?
(b) How many nearest neighbors does each S2− have?
(c) what angle is made by the line connecting any Zn2+ to any two of its nearest neighbors ?
(d) What minimum r+/r− ratio is needed to avoid anion -anion contact, if closest cation-anion pairs are assumed to touch ?AC.N. of Zn2+ & S2−=4 & 4BC.N. of Zn2+ & S2− = 6 & 6C109∘28DrZn2+rS2−=0.225CsCl structure is given below , Assign all contact with cation and anions are also contact with neighbouring anion [KLMN vertical diagonal plane KLO right angle triangle ]
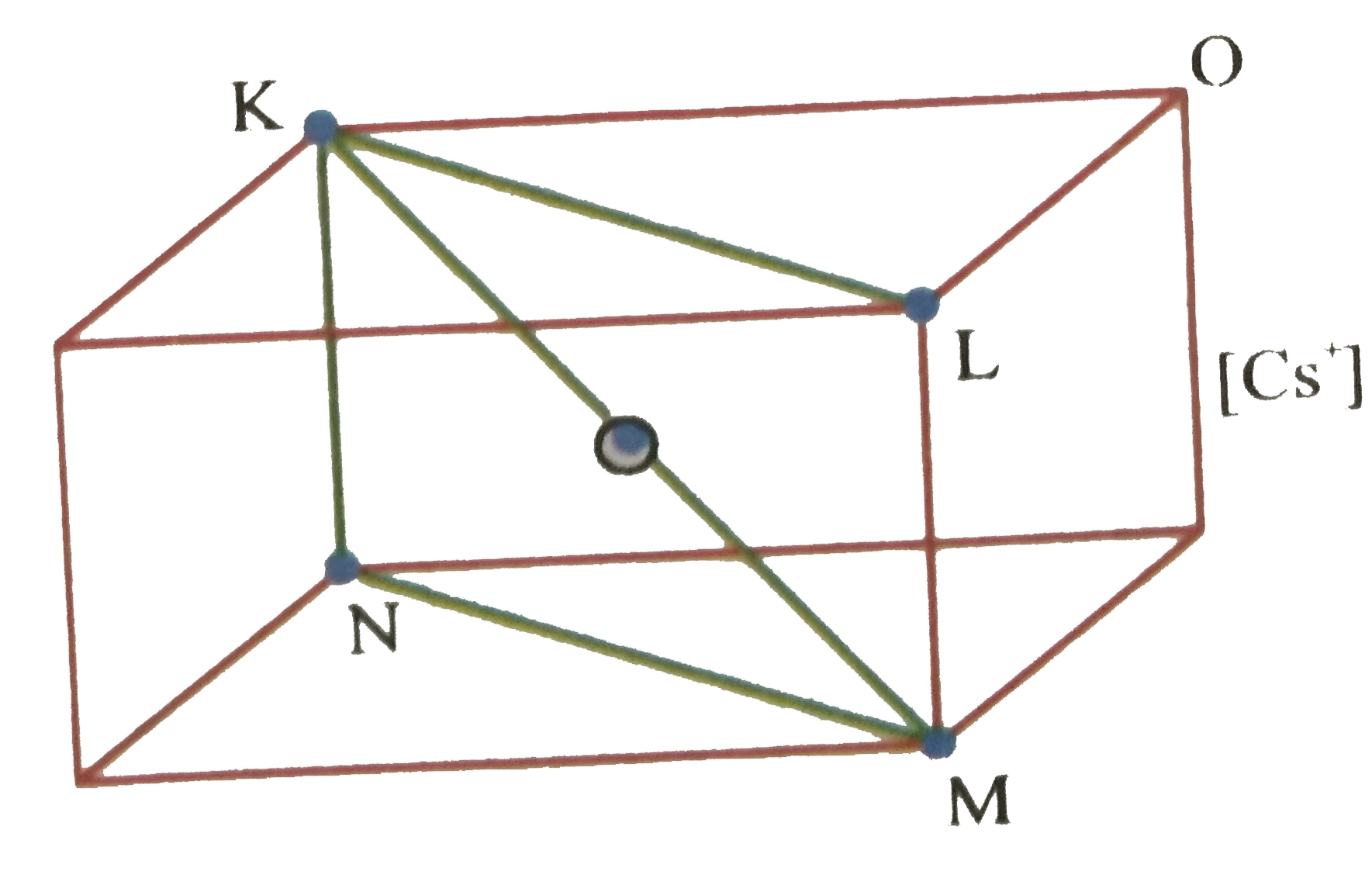
rCl−rCl−A0.734B0.99C1.36D0.225
KBr crystallizes in NaCl type of unit cell. K+ radius =1.33Å,Br− radius =1.95Å
(a) How many K+ ions and how many Br− ions are in each unit cell ?
(b) Assuming the additivity of ionic radii, what is a ?
(c) Calculate the density of a perfect KBr crystal
(d) What minimum value of r+/r− is needed to prevent anion-anion contact in this structure
View SolutionKBr crystallizes in NaCl type of unit cell. K+ radius =1.33Å,Br− radius =1.95Å
(a) How many K+ ions and how many Br− ions are in each unit cell ?
(b) Assuming the additivity of ionic radii, what is a ?
(c) Calculate the density of a perfect KBr crystal
(d) What minimum value of r+/r− is needed to prevent anion-anion contact in this structure
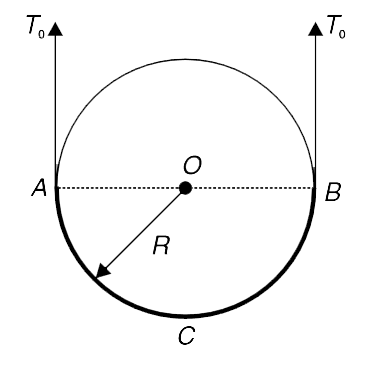
View SolutionA smooth cylinder is fixed with its axis horizontal. Radius of the cylinder is R. A uniform rope (ACB) of linear mass density λ (kg/m) is exactly of length πR and is held in semicircular shape in vertical plane around the cylinder as shown in figure. Two massless strings are connected at the two ends of the rope and are pulled up vertically with force T0 to keep the rope in contact with the cylinder.
(a) Find minimum value of T0 so that the rope does not lose contact with the cylinder at any point.
(b) If T0 is decreased slightly below the minimum value calculated in (a), where will the rope lose contact with the cylinder.
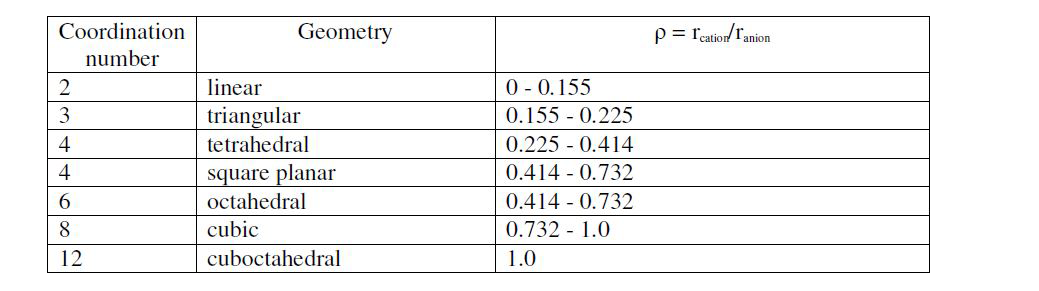
View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
A solid AB has square planar structure. If the radius of cation A+ is 120pm,Calculate the maximum possible value of anion B−
View SolutionConsider eight small spheres , radius = rs arranged at the corner of the cube , they are small enough so that they are not in contact . Now place a larger sphere , radius = rl at the centre of the cube . This sphere is just large enough so that it is in contact with the eight small sphere . Now let the radius of the large sphere shrink , but keep the small sphere in contact with it . what is the radius ratio rs/rl, when the small spheres at the cube corners come in to contact with each other .

View Solution
