A blown-up balloon has a volume of 500 mL at 5∘C . The balloon is distended to 7/8 of its maximum stretching capacity. Will the balloon burst at 30∘C? Determine the minimum temperature above which it will burst.
To solve the problem, we will use the ideal gas law and the concept of volume expansion with temperature. The key relationship we will use is Charles's Law, which states that the volume of a gas is directly proportional to its temperature (in Kelvin) when pressure is constant.
1. Identify Initial Conditions:
- Initial volume of the balloon, V1=500mL
- Initial temperature, T1=5∘C=5+273.15=278.15K
2. Determine the Maximum Volume:
- The balloon is distended to 78 of its maximum capacity. Since the current volume is 500 mL, we can denote the maximum volume as Vmax.
- Therefore, 78Vmax=500mL
- Solving for Vmax:
Vmax=500×87=40007≈571.43mL
3. Calculate the Volume at 30°C:
- We need to check if the balloon will burst at 30∘C.
- Convert 30∘C to Kelvin:
T2=30+273.15=303.15K
4. Use Charles's Law to Find New Volume:
- According to Charles's Law:
V1T1=V2T2
- Rearranging to find V2:
V2=V1×T2T1=500×303.15278.15
- Calculating V2:
V2≈500×1.090=545.25mL
5. Determine if the Balloon Will Burst:
- The balloon will burst if V2 exceeds the maximum volume Vmax.
- Since Vmax≈571.43mL and V2≈545.25mL, the balloon will not burst at 30∘C.
6. Determine the Minimum Temperature for Bursting:
- To find the temperature at which the balloon will burst, set V2=Vmax:
Vmax=V1×TburstT1
- Rearranging gives:
Tburst=T1×VmaxV1=278.15×571.43500
- Calculating Tburst:
Tburst≈278.15×1.14286≈318.15K
- Converting back to Celsius:
Tburst≈318.15−273.15=45∘C
Final Answer:
The balloon will not burst at 30∘C. The minimum temperature above which it will burst is approximately 45∘C.
- Initial volume of the balloon, V1=500mL
- Initial temperature, T1=5∘C=5+273.15=278.15K
- The balloon is distended to 78 of its maximum capacity. Since the current volume is 500 mL, we can denote the maximum volume as Vmax.
- Therefore, 78Vmax=500mL
- Solving for Vmax:
Vmax=500×87=40007≈571.43mL
- We need to check if the balloon will burst at 30∘C.
- Convert 30∘C to Kelvin:
T2=30+273.15=303.15K
- According to Charles's Law:
V1T1=V2T2
- Rearranging to find V2:
V2=V1×T2T1=500×303.15278.15
- Calculating V2:
V2≈500×1.090=545.25mL
- The balloon will burst if V2 exceeds the maximum volume Vmax.
- Since Vmax≈571.43mL and V2≈545.25mL, the balloon will not burst at 30∘C.
- To find the temperature at which the balloon will burst, set V2=Vmax:
Vmax=V1×TburstT1
- Rearranging gives:
Tburst=T1×VmaxV1=278.15×571.43500
- Calculating Tburst:
Tburst≈278.15×1.14286≈318.15K
- Converting back to Celsius:
Tburst≈318.15−273.15=45∘C
The balloon will not burst at 30∘C. The minimum temperature above which it will burst is approximately 45∘C.
Topper's Solved these Questions
Similar Questions
A ballon blown up with 1 mole of gas has a volume of 480mL at 5∘C The balloon is filled to (7/8) th of its maximum capacity Suggest
(a) Will the balloon burst at 30∘C
(b) The minimum temperature at which it will burst
(c ) The pressure of gas inside the balloon at 5∘C
(d) The pressure of gas when balloon bursts .View SolutionA toy balloon blown up at 5∘C has a volume of 480 mL. At this stage, the balloon is distended to 7/8th of its maximum stretching capacity.
(i) Will the balloon burst if it is brought to a room having temperature 30∘C?
(ii) Calculate the temperature at which the balloon will burst.View Solution
Knowledge Check
- Question 1 - Select One
A bolloon blown up has a volume of 300 mL at 27% C. The balloon is distended to 56 of its maximum stretching capacity. The maximum temperature above which it will burst is
A77∘CB67∘CC57∘CD87∘C - Question 2 - Select One
On the surface of the earth at 1 atm pressure, a balloon filled with H2 gas occupies 500mL. This volume is 56 of its maximum capacity. The balloon is left in air. It starts rising. The height above which the balloon will burst if temperature of the atmospere remains constant and the pressure decreases 1 mm for every 100cm rise of height is:
A120mB136.67mC126.67mD100m - Question 3 - Select One
Two balloon A and B are taken at 300 K. Maximum capacity of balloon A and balloon B are 800 mL and 1800 mL respectively. When the balloon system is heated, which one will burst first ?
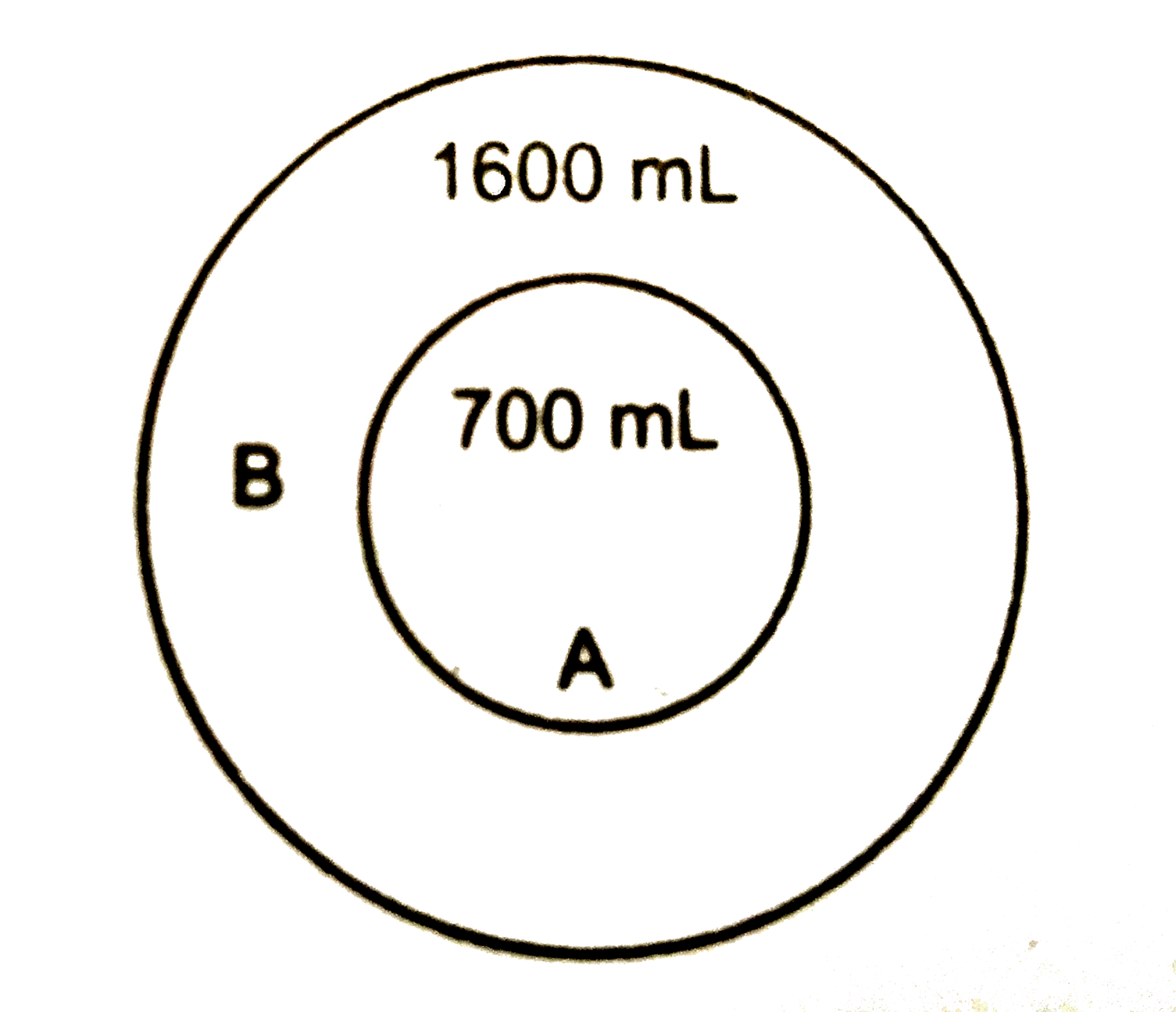 AInner balloon ABOuter balloon BCBoth balloon's simultaneouslyDcannot be predicted
AInner balloon ABOuter balloon BCBoth balloon's simultaneouslyDcannot be predicted
On the surface of the earth at 1 atm pressure, a balloon filled with H2 gas occupies 500mL. This volume is 56 of its maximum capacity. The balloon is left in air. It starts rising. The height above which the balloon will burst if temperature of the atmospere remains constant and the pressure decreases 1 mm for every 100cm rise of height is:
View SolutionA balloon has 5.0 mole of helium at 7∘C. Calculate
(a) the number of atoms of helium in the balloon.
(b) the total internal energy of the system.View SolutionA ballon has 5.0 g mole of helium at 7∘C Calculate
(a) the number of atoms of helium in the balloon,
(b) the total internal energy of the system.View SolutionTwo inflated ballons I and II (thin skin) having volume 600 mL and 1500 mL at 300 K are taken as shown in diagram. If maximum volume of inner and outer balloons are 800 mL and 1800 mL respectively then find the balloon which will burst first on gradual heating.
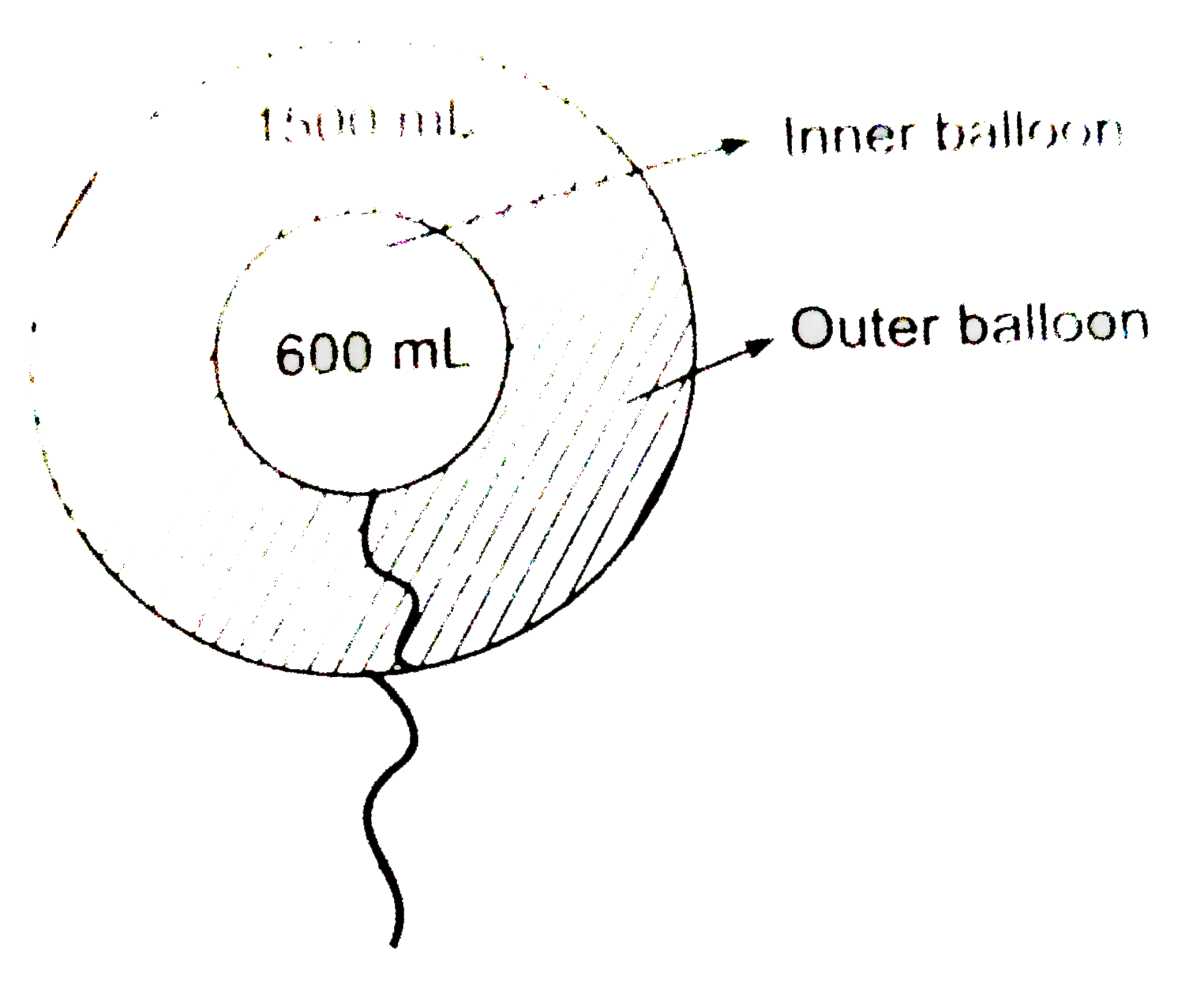 View Solution
View SolutionA cylinder with a movable piston is filled at 25∘C with a gas that occupies a volume of 30.5cm3. If the maximum capacity of the cylinder is 45.8cm3, what is the highest temperature to which the cylinder can be heated at constant pressure without having the piston come out?
View Solution

