ABC×D∃D=ABCABC find D+E = ?
The correct Answer is:=4
To solve the equation ABC×DEED=ABCABC, we can follow these steps:
Step 1: Understand the structure of the numbers
The number ABC represents a three-digit number, where A,B, and C are its digits. The number DEED represents a four-digit number, where D and E are its digits. The number ABCABC is formed by repeating the three-digit number ABC twice.
Step 2: Express DEED in terms of ABC
The number DEED can be expressed as:
DEED=1000D+100E+10E+D=1001D+110E
Step 3: Express ABCABC in terms of ABC
The number ABCABC can be expressed as:
ABCABC=1000×ABC+ABC=1001×ABC
Step 4: Set up the equation
From the problem statement, we have:
ABC×(1001D+110E)=1001×ABC
Step 5: Simplify the equation
Assuming ABC≠0 (since it's a three-digit number), we can divide both sides by ABC:
1001D+110E=1001
Step 6: Rearrange the equation
Rearranging gives us:
1001D+110E−1001=0
Step 7: Solve for D and E
This can be rewritten as:
1001D+110E=1001
To find integer values for D and E, we can try different values for D (from 0 to 9) and solve for E.
1. If D=1:
1001(1)+110E=1001⟹110E=0⟹E=0
Thus, we have D=1 and E=0.
Step 8: Calculate D+E
Now, we can find D+E:
D+E=1+0=1
Final Answer
Thus, the final answer is:
D+E=1
---
The number ABC represents a three-digit number, where A,B, and C are its digits. The number DEED represents a four-digit number, where D and E are its digits. The number ABCABC is formed by repeating the three-digit number ABC twice.
The number DEED can be expressed as:
DEED=1000D+100E+10E+D=1001D+110E
The number ABCABC can be expressed as:
ABCABC=1000×ABC+ABC=1001×ABC
From the problem statement, we have:
ABC×(1001D+110E)=1001×ABC
Assuming ABC≠0 (since it's a three-digit number), we can divide both sides by ABC:
1001D+110E=1001
Rearranging gives us:
1001D+110E−1001=0
This can be rewritten as:
1001D+110E=1001
To find integer values for D and E, we can try different values for D (from 0 to 9) and solve for E.
1001(1)+110E=1001⟹110E=0⟹E=0
Now, we can find D+E:
D+E=1+0=1
Thus, the final answer is:
D+E=1
Topper's Solved these Questions
- NUMBER SYSTEM BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - NUMBER SYSTEM EXERCISE - MULTIPLE CHOICE QUESTIONS
225 Videos
- MOCK TEST IIBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - MOCK TEST IIEXERCISE - MCQ
100 Videos
- PARTNERSHIPBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PARTNERSHIPEXERCISE - Questions
26 Videos
Similar Questions
Knowledge Check
In ABCABC packing of atoms, which of the following cubic lattice has 74% space occupied by the atoms?
ABody centred cubic latticeBSimple cubic latticCHexagonal closed latticeDCubic closed lattice
In Fig. 4.95, if ∠ADE=∠B show that ADE~ABC . If AD=3.8cm , AE=3.6cm , BE=2.1cm and BC=4.2cm , find DE . (FIGURE)
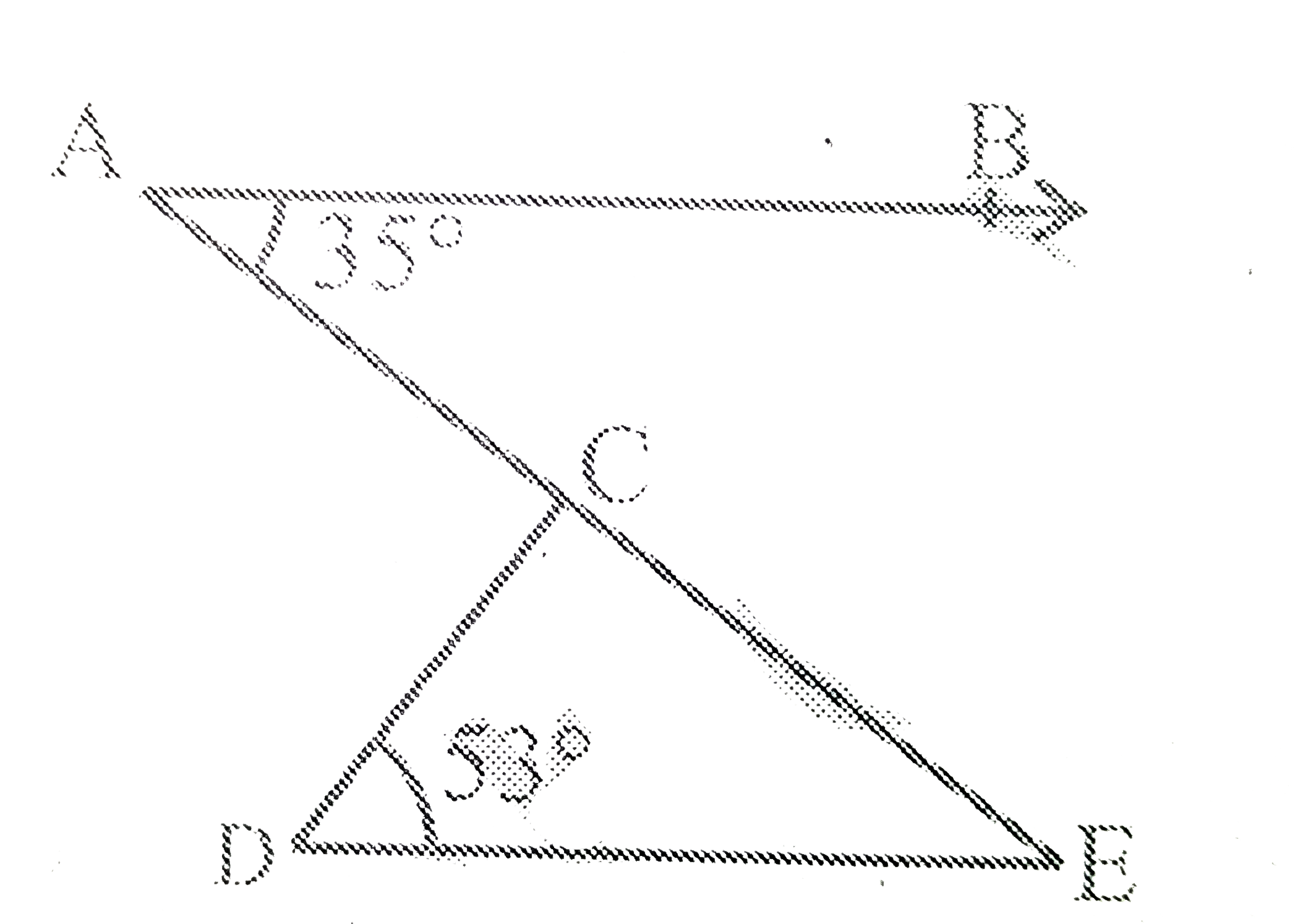
View SolutionIn Fig.87, the corresponding arms of ∠ABC and ∠DEF are parallel. If ∠ABC=750, find the ∠DEF.
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=4 , AE=8 , DB=x−4 , and EC=3x−19 , find x (ii) If AD=8 cm , AB=12cm and AE=12 cm , find CE . (iii) If AD=4 cm , DB=4.5 cm and AE=8 cm , find AC .
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=6 cm , DB=9 cm and AE=8 cm , find AC . (ii) If ADDB=34 and AC=15 cm , find AE . (iii) If ADDB=23 and AC=18 cm , find AE .
View SolutionIn a ABC , D and E are points on AB and AC respectively such that DE/BC . If AD=2.4cm, AE=3.2cm, DE=2cm and BC=5cm , find BD and CE .
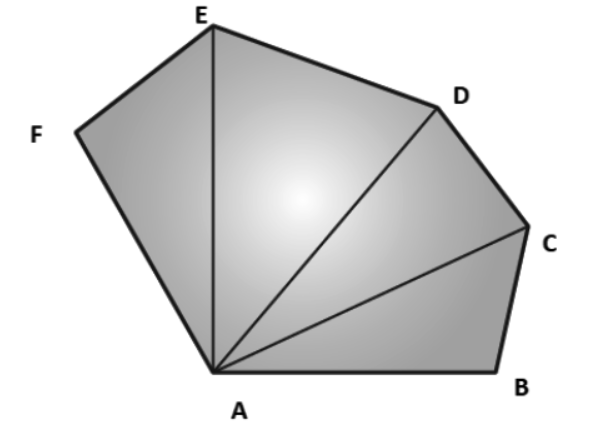
View SolutionIn the six cornered figure, (fig.20), AC,AD and AE are joined. Find ∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA.
View Solution