ABC × DEED = ABCABC Find D + E = ? Where A,B,C,D,E are digits.
To solve the problem ABC×DEED=ABCABC, we will follow these steps:
Step 1: Understand the structure of the numbers
- Let ABC represent a three-digit number where A,B,C are its digits.
- The number DEED can be expressed as 1000D+100E+10E+D=1001D+110E.
- The number ABCABC can be expressed as 1000×ABC+ABC=1001×ABC.
Step 2: Set up the equation
From the above understanding, we can set up the equation:
ABC×(1001D+110E)=1001×ABC
Step 3: Simplify the equation
Since ABC is common on both sides, we can divide both sides by ABC (assuming ABC≠0):
1001D+110E=1001
Step 4: Rearranging the equation
Now, we can rearrange the equation:
1001D+110E=1001
Subtract 1001D from both sides:
110E=1001−1001D
Step 5: Solve for E
Now we can express E:
E=1001−1001D110
Step 6: Find possible values for D and E
Since D and E are digits (0-9), we can test values for D:
- If D=1:
E=1001−1001×1110=0110=0
This gives us D=1 and E=0.
Step 7: Calculate D+E
Now we can find D+E:
D+E=1+0=1
Final Answer
Thus, the value of D+E is 1.
---
- Let ABC represent a three-digit number where A,B,C are its digits.
- The number DEED can be expressed as 1000D+100E+10E+D=1001D+110E.
- The number ABCABC can be expressed as 1000×ABC+ABC=1001×ABC.
From the above understanding, we can set up the equation:
ABC×(1001D+110E)=1001×ABC
Since ABC is common on both sides, we can divide both sides by ABC (assuming ABC≠0):
1001D+110E=1001
Now, we can rearrange the equation:
1001D+110E=1001
Subtract 1001D from both sides:
110E=1001−1001D
Now we can express E:
E=1001−1001D110
Since D and E are digits (0-9), we can test values for D:
- If D=1:
E=1001−1001×1110=0110=0
This gives us D=1 and E=0.
Now we can find D+E:
D+E=1+0=1
Thus, the value of D+E is 1.
Similar Questions
Knowledge Check
C E B A C D B C D A C E B E D C A B A D A C E D U B A U B D B U
How many such D's are there in the given arrangement each of which is immediately preceded by a consonant and also immediately followed by a vowel?AMore than fourBfourCTwoDOneC E B A C D B C D A C E B E D C A B A D A C E D U B A U B D B U
How many such A's are there in the given arrangement each of which is immediately preceded by a 'B' and also immediately followed by a consonant?AOneBNoneCMore than threeDTwoC E B A C D B C D A C E B E D C A B A D A C E D U B A U B D B U Which of the following is the ninth to the right of the twenty- second from the right end of the given arrangement?
ADBECBDC
Calculate the area of the pentagon ABCDE , where AB=AE and with dimensions as shown in Fig.36.
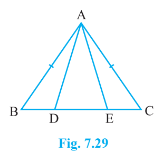
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
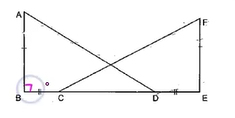
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
View SolutionB U B D C E D B D E U B A D C B E A C D A E B A U A C D B C A C
If all A's are dropped from the above arrangement, which of the following will be eleventh from the right end of the above arrangement
View SolutionB U B D C E D B D E U B A D C B E A C D A E B A U A C D B C A C
Which of the following is the eighth to the left of the twentieth from the left end of the above arrangement?
View Solution
