The marks obtained by Vijay and Amith are in the ratio 4:5 and those obtained by Amith and Abhishek in the ratio of 3:2. The marks obtained by Vijay and Abhishek are in the ratio of ?
A) 4:5
B) 6:5
C) 3:2
D) 1:3
To solve the problem, we need to find the ratio of marks obtained by Vijay and Abhishek based on the given ratios of marks obtained by Vijay and Amith, and Amith and Abhishek.
1. Identify the Given Ratios:
- The ratio of marks obtained by Vijay and Amith is given as 4:5.
- The ratio of marks obtained by Amith and Abhishek is given as 3:2.
2. Express the Ratios in Terms of a Common Variable:
- Let the marks obtained by Vijay be 4x and those obtained by Amith be 5x (from the first ratio).
- Let the marks obtained by Amith be 3y and those obtained by Abhishek be 2y (from the second ratio).
3. Equate the Marks of Amith:
- Since Amith's marks are represented in both ratios, we can set 5x=3y.
4. Solve for One Variable in Terms of the Other:
- From 5x=3y, we can express y in terms of x:
y=53x
5. Substitute y Back into the Expression for Abhishek's Marks:
- Now, substitute y into the expression for Abhishek's marks:
Abhishek's marks=2y=2(53x)=103x
6. Now, We Have the Marks for Vijay and Abhishek:
- Vijay's marks = 4x
- Abhishek's marks = 103x
7. Find the Ratio of Vijay's Marks to Abhishek's Marks:
- The ratio of Vijay's marks to Abhishek's marks is:
Ratio=4x103x=4x⋅310x=1210=65
8. Final Answer:
- Therefore, the ratio of marks obtained by Vijay and Abhishek is 6:5.
- The ratio of marks obtained by Vijay and Amith is given as 4:5.
- The ratio of marks obtained by Amith and Abhishek is given as 3:2.
- Let the marks obtained by Vijay be 4x and those obtained by Amith be 5x (from the first ratio).
- Let the marks obtained by Amith be 3y and those obtained by Abhishek be 2y (from the second ratio).
- Since Amith's marks are represented in both ratios, we can set 5x=3y.
- From 5x=3y, we can express y in terms of x:
y=53x
- Now, substitute y into the expression for Abhishek's marks:
Abhishek's marks=2y=2(53x)=103x
- Vijay's marks = 4x
- Abhishek's marks = 103x
- The ratio of Vijay's marks to Abhishek's marks is:
Ratio=4x103x=4x⋅310x=1210=65
- Therefore, the ratio of marks obtained by Vijay and Abhishek is 6:5.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The marks obtained by E in Geography are what per cent of the marks obtained by E in Hindi?
A45%B55%C59%D60%What are the average marks obtained by the student?
A57B63C80D48A phenotypic ratio not obtained by Mendel was
A3:1B1:2:1C1:1:1:1D9:3:3:1
The given pie chart shows the marks obtained (in degrees) by a student in different subjects . The total marks obtained by the student in the examination is 432.
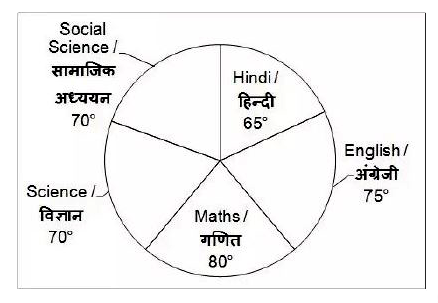
The marks obtained in Maths is how much percent more than the marks obtained in Science?
View SolutionThe given pie-chart shows the marks obtained (in degrees) by a student in different subjects. The total marks obtained by the student in the examination is 432.
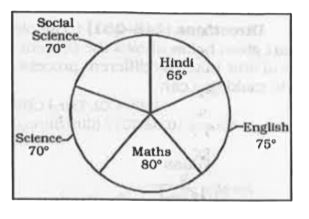
The marks obtained in Science in what percentage of the total marks?
View SolutionThe given pie-chart shows the marks obtained (in degrees) by a student in different subjects. The total marks obtained by the student in the examination is 432.

The marks obtained in Science in what percentage of the total marks?
View SolutionIn a monthly unit test, the marks scored by Bunny and Sunny are in the ratio of 10:7 and those scored by Bharat and Sunny are in the ratio of 8:9. If Bharat 112 marks, then find the marks scored by Bunny.
View SolutionThe given pie-chart shows the marks obtained (in degrees) by a student in different subjects. The total marks obtained by the student in the examination is 432.
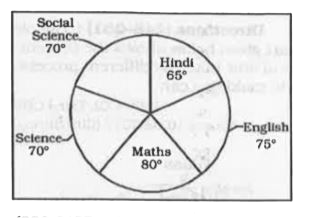
The marks obtained in Maths is how much per cent more than the marks obtained in Social Science?
View Solution
