Find the area of a trapezium ABCD in which AB || DC, AB = 26cm, BC = 25cm, CD = 40cm and DA = 25cm.
648cm2
792cm2
660cm2
798cm2
The correct Answer is:B
To find the area of trapezium ABCD where AB || DC, we can use the following steps:
Step 1: Identify the given dimensions
We have:
- AB = 26 cm (one of the parallel sides)
- DC = 40 cm (the other parallel side)
- BC = 25 cm (one of the non-parallel sides)
- DA = 25 cm (the other non-parallel side)
Step 2: Calculate the height of the trapezium
To find the height (h) of the trapezium, we can drop perpendiculars from points B and A to line DC, meeting at points E and F respectively. This will create two right triangles, ADF and BCE.
Using the Pythagorean theorem in triangle ADF:
- AF = h (height)
- AD = 25 cm
- DF = DC - AB = 40 cm - 26 cm = 14 cm (the base of triangle ADF)
Thus, we can write:
AD2=AF2+DF2
252=h2+142
625=h2+196
h2=625−196
h2=429
h=√429≈20.7cm
Step 3: Calculate the area of the trapezium
The area (A) of a trapezium can be calculated using the formula:
A=12×(AB+DC)×h
Substituting the values we have:
A=12×(26+40)×√429
A=12×66×√429
A=33×√429
Calculating √429≈20.7:
A≈33×20.7≈683.1cm2
Final Answer
The area of trapezium ABCD is approximately 683.1 cm².
---
We have:
- AB = 26 cm (one of the parallel sides)
- DC = 40 cm (the other parallel side)
- BC = 25 cm (one of the non-parallel sides)
- DA = 25 cm (the other non-parallel side)
To find the height (h) of the trapezium, we can drop perpendiculars from points B and A to line DC, meeting at points E and F respectively. This will create two right triangles, ADF and BCE.
- AF = h (height)
- AD = 25 cm
- DF = DC - AB = 40 cm - 26 cm = 14 cm (the base of triangle ADF)
AD2=AF2+DF2
252=h2+142
625=h2+196
h2=625−196
h2=429
h=√429≈20.7cm
The area (A) of a trapezium can be calculated using the formula:
A=12×(AB+DC)×h
Substituting the values we have:
A=12×(26+40)×√429
A=12×66×√429
A=33×√429
Calculating √429≈20.7:
A≈33×20.7≈683.1cm2
The area of trapezium ABCD is approximately 683.1 cm².
Topper's Solved these Questions
- QUADRILATERALBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - QUADRILATERALEXERCISE - EXERCISE
48 Videos
- PROFIT & LOSSBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PROFIT & LOSSEXERCISE - Questions
200 Videos
- RATIO & PROPORTIONBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - RATIO & PROPORTIONEXERCISE - QUESTIONS
113 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
A80∘B100∘C120∘D140∘Find the area of a parallelogram ABCD in which AB = 8 cm, BC = 15 cm and diagonal AC = 17 cm.
A220cm2B150cm2C120cm2D175cm2ABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
A80∘B100∘C120∘D140∘
Construct a trapezium ABCD in which AB||DC, ∠A = 105°, AD = 3 cm, AB = 4 cm and CD = 8 cm.
View SolutionFind the area of quadrilateral ABCD in which ∠B=90∘, BC = 32 cm, AB = 24 cm and CD=DA = 25 cm.
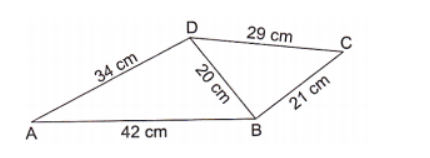
View SolutionFind the area of the quadrilateral ABCD in which in AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and diagonal BD = 20 cm.
View SolutionFind the area of the quadrilateral ABCD, in which AB=7cm, BC=6cm, CD=12 cm, DA=15cm and AC=9 cm.
View SolutionFind the area of the quadrilateral ABCD , in which AB=7cm,BC=6cm,CD=12cm,DA=15cmandAC=9cm
View Solution
