In a quadrilateral ABCD, OA and OB are the angle bi- sectors of ∠DABand∠CBA. If∠ADC=70 and ∠ BCD= 80 then find the angle AOB
70∘
80∘
90∘
75∘
The correct Answer is:D
To find the angle AOB in the quadrilateral ABCD, where OA and OB are the angle bisectors of angles DAB and CBA respectively, we can follow these steps:
Step 1: Understand the given angles
We are given:
- ∠ADC = 70°
- ∠BCD = 80°
Step 2: Define the angles at points A and B
Let:
- ∠DAB = 2x (since OA is the angle bisector)
- ∠CBA = 2y (since OB is the angle bisector)
Step 3: Use the property of quadrilaterals
The sum of all angles in a quadrilateral is 360°. Therefore, we can set up the equation:
∠DAB+∠ABC+∠BCD+∠ADC=360°
Substituting the angles we have:
2x+2y+80°+70°=360°
Step 4: Simplify the equation
Combine the known angles:
2x+2y+150°=360°
Subtract 150° from both sides:
2x+2y=210°
Dividing the entire equation by 2 gives:
x+y=105°
Step 5: Find angle AOB
In triangle AOB, we know that:
∠AOB=180°−(∠DAB+∠CBA)=180°−(2x+2y)
Substituting x+y=105°:
∠AOB=180°−2(x+y)=180°−2(105°)=180°−210°=−30°
This indicates an error in the calculation. Let's correct it.
Correct Calculation for angle AOB
Since we need to find ∠AOB:
∠AOB=180°−(x+y)
Substituting x+y=105°:
∠AOB=180°−105°=75°
Final Answer
Thus, the angle AOB is:
∠AOB=75°
---
We are given:
- ∠ADC = 70°
- ∠BCD = 80°
Let:
- ∠DAB = 2x (since OA is the angle bisector)
- ∠CBA = 2y (since OB is the angle bisector)
The sum of all angles in a quadrilateral is 360°. Therefore, we can set up the equation:
∠DAB+∠ABC+∠BCD+∠ADC=360°
Substituting the angles we have:
2x+2y+80°+70°=360°
Combine the known angles:
2x+2y+150°=360°
Subtract 150° from both sides:
2x+2y=210°
Dividing the entire equation by 2 gives:
x+y=105°
In triangle AOB, we know that:
∠AOB=180°−(∠DAB+∠CBA)=180°−(2x+2y)
Substituting x+y=105°:
∠AOB=180°−2(x+y)=180°−2(105°)=180°−210°=−30°
This indicates an error in the calculation. Let's correct it.
Since we need to find ∠AOB:
∠AOB=180°−(x+y)
Substituting x+y=105°:
∠AOB=180°−105°=75°
Thus, the angle AOB is:
∠AOB=75°
Topper's Solved these Questions
Similar Questions
In quadrilateral ABCD, BA = BC and DA = DC. Prove that BD bisects ∠ ABC as well as ∠ ADC.
View SolutionIn quadrilateral ABCD, ∠C=72∘and∠D=28∘. The bisectors of ∠Aand∠B meet in O. What is the measure of ∠AOB? एक चतुरभुज ABCD में, angle C = 72^circ और angle D = 28^circहै। ∠Aऔर∠B के द्विभाजक O पर मिलते हैं। ∠AOB की माप क्या होगी?
View Solution
Knowledge Check
- Question 1 - Select One
In a quadrilateral ABCD, OA and OB are the angle bisectors of ∠DAB and ∠CBA. If ∠ADC=70∘ and ∠BCD=80∘ then find ∠AOB ?
A70∘B80∘C90∘D75∘ - Question 2 - Select One
In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively, ∠C=70∘and∠D=30∘. Then, ∠AOB=?
A50∘B130∘C80∘D100∘ - Question 3 - Select One
In a quadrilateral ABCD, the bisectors of ∠A and ∠B meet at O. If ∠C=70∘and∠D=130∘, then measure of ∠AOBis
A40∘B60∘C80∘D100∘
In cyclic quadrilateral ABCD, Diagonals AC and BD intersect at P. If ∠DBC=70∘ and ∠BAC=30∘ then find ∠BCD
View SolutionABCD is a quadrilateral in which AB=BC and AD =CD ,Show that BD bisects boht the angle ABC and ADC
View SolutionIn the given figure ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC=55∘and∠BAC=45∘, find ∠BCD.
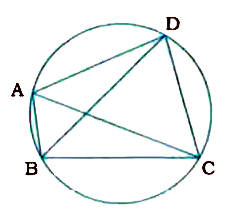 View Solution
View SolutionIn the quadrilateral ABCD shown below, ∠DAB=∠DCX=120∘. If ∠ABC=105∘, then what is the value of ∠ADC?
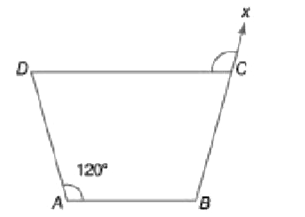 View Solution
View Solution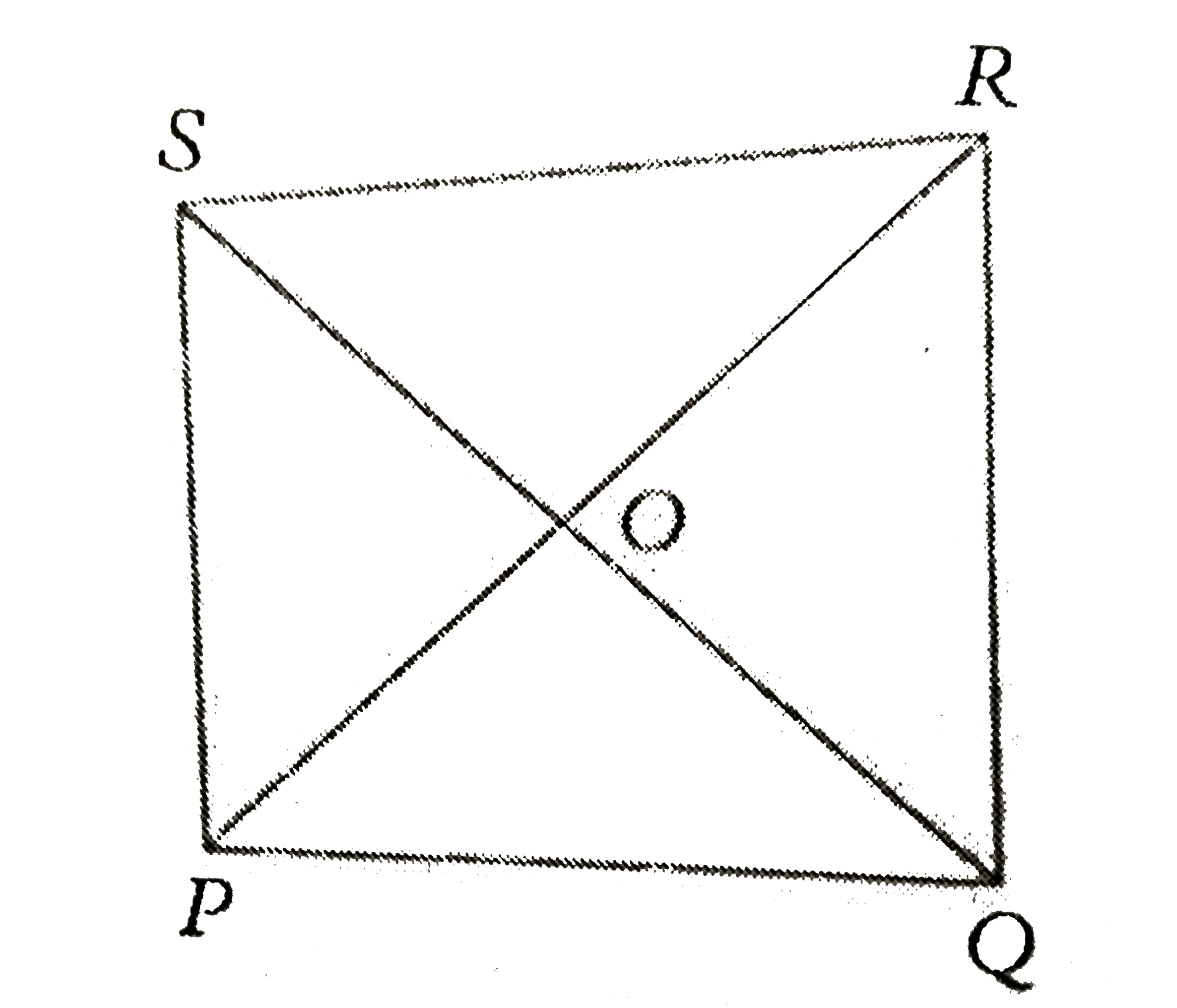
In the given figure, PQRS is a quadrilateral ,PR and QS intersect at O. If ∠PQR=70∘,∠SPQ=80∘,and∠PRQ=60∘, then find ∠SPR.View Solution

