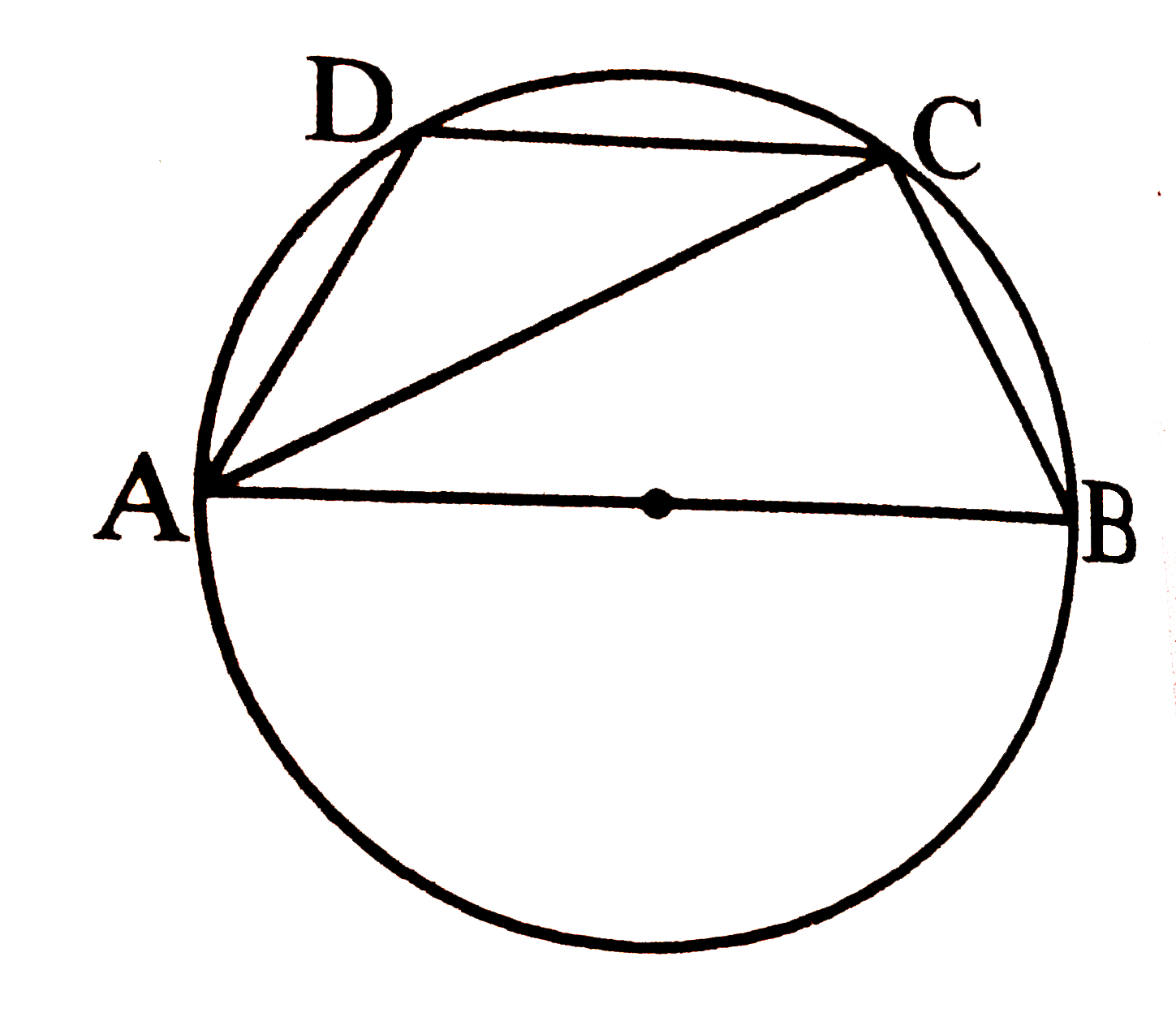Question

ABCD is a cyclic quadrilateral in which AB is a diameter , $,BC=CD\text{and}\angle ABD={50}^{\circ }$ then $\angle DBC$ is :

Options

A. `25^(@)`
B. `20^(@)`
C. `45^(@)`
D. `30^(@)`

Answer

B

Explanation

To solve the problem, we will follow these steps:

1. Identify the Given Information: We have a cyclic quadrilateral ABCD where AB is a diameter, BC = CD, and ∠ABD = 50°.

2. Use the Property of Cyclic Quadrilaterals: Since AB is a diameter, ∠ADB will be a right angle (90°) because the angle subtended by a diameter at the circumference is always 90°.

\( \angle ADB = 90° \)

3. Find Angle DAB: In triangle ADB, we know that the sum of angles in a triangle is 180°. Thus, we can find angle DAB as follows:

\( \angle DAB + \angle ABD + \angle ADB = 180° \)

Substituting the known values:

\( \angle DAB + 50° + 90° = 180° \)

Simplifying this gives:

\( \angle DAB + 140° = 180° \)

\( \angle DAB = 180° - 140° = 40° \)

4. Use the Opposite Angles Property: In a cyclic quadrilateral, the sum of opposite angles is 180°. Therefore, we can find angle BCD:

\( \angle DAB + \angle BCD = 180° \)

Substituting the value of angle DAB:

\( 40° + \angle BCD = 180° \)

Solving for angle BCD gives:

\( \angle BCD = 180° - 40° = 140° \)

5. Find Angle DBC: In triangle BCD, since BC = CD, triangle BCD is isosceles. Let angle DBC = angle BDC = θ. Therefore:

\( \theta + \theta + 140° = 180° \)

Simplifying this gives:

\( 2\theta + 140° = 180° \)

\( 2\theta = 180° - 140° = 40° \)

\( \theta = \frac{40°}{2} = 20° \)

Thus, angle DBC is:

\( \angle DBC = 20° \)

Final Answer: The value of angle DBC is 20°.

---