ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠CAB=48∘, then what is the value (in degrees) of ∠ADC?
52
77
138
142
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the properties of the cyclic quadrilateral
A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle. One important property of cyclic quadrilaterals is that the opposite angles sum up to 180 degrees.
Step 2: Identify the given information
We are given that:
- ABCD is a cyclic quadrilateral.
- AB is the diameter of the circle.
- Angle CAB = 48 degrees.
Step 3: Use the inscribed angle theorem
Since AB is the diameter, angle ACB (the angle opposite to the diameter) is a right angle (90 degrees). This is due to the inscribed angle theorem, which states that an angle inscribed in a semicircle is a right angle.
Step 4: Calculate angle CBA
In triangle ABC, we can use the fact that the sum of angles in a triangle is 180 degrees:
Angle CAB+Angle ACB+Angle CBA=180∘
Substituting the known values:
48∘+90∘+Angle CBA=180∘
This simplifies to:
Angle CBA=180∘−48∘−90∘=42∘
Step 5: Use the property of cyclic quadrilaterals
Now, since ABCD is a cyclic quadrilateral, we know that:
Angle CBA+Angle ADC=180∘
Substituting the value of angle CBA:
42∘+Angle ADC=180∘
Solving for angle ADC:
Angle ADC=180∘−42∘=138∘
Final Answer
The value of angle ADC is 138 degrees.
---
A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle. One important property of cyclic quadrilaterals is that the opposite angles sum up to 180 degrees.
We are given that:
- ABCD is a cyclic quadrilateral.
- AB is the diameter of the circle.
- Angle CAB = 48 degrees.
Since AB is the diameter, angle ACB (the angle opposite to the diameter) is a right angle (90 degrees). This is due to the inscribed angle theorem, which states that an angle inscribed in a semicircle is a right angle.
In triangle ABC, we can use the fact that the sum of angles in a triangle is 180 degrees:
Angle CAB+Angle ACB+Angle CBA=180∘
Substituting the known values:
48∘+90∘+Angle CBA=180∘
This simplifies to:
Angle CBA=180∘−48∘−90∘=42∘
Now, since ABCD is a cyclic quadrilateral, we know that:
Angle CBA+Angle ADC=180∘
Substituting the value of angle CBA:
42∘+Angle ADC=180∘
Solving for angle ADC:
Angle ADC=180∘−42∘=138∘
The value of angle ADC is 138 degrees.
Similar Questions
In the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
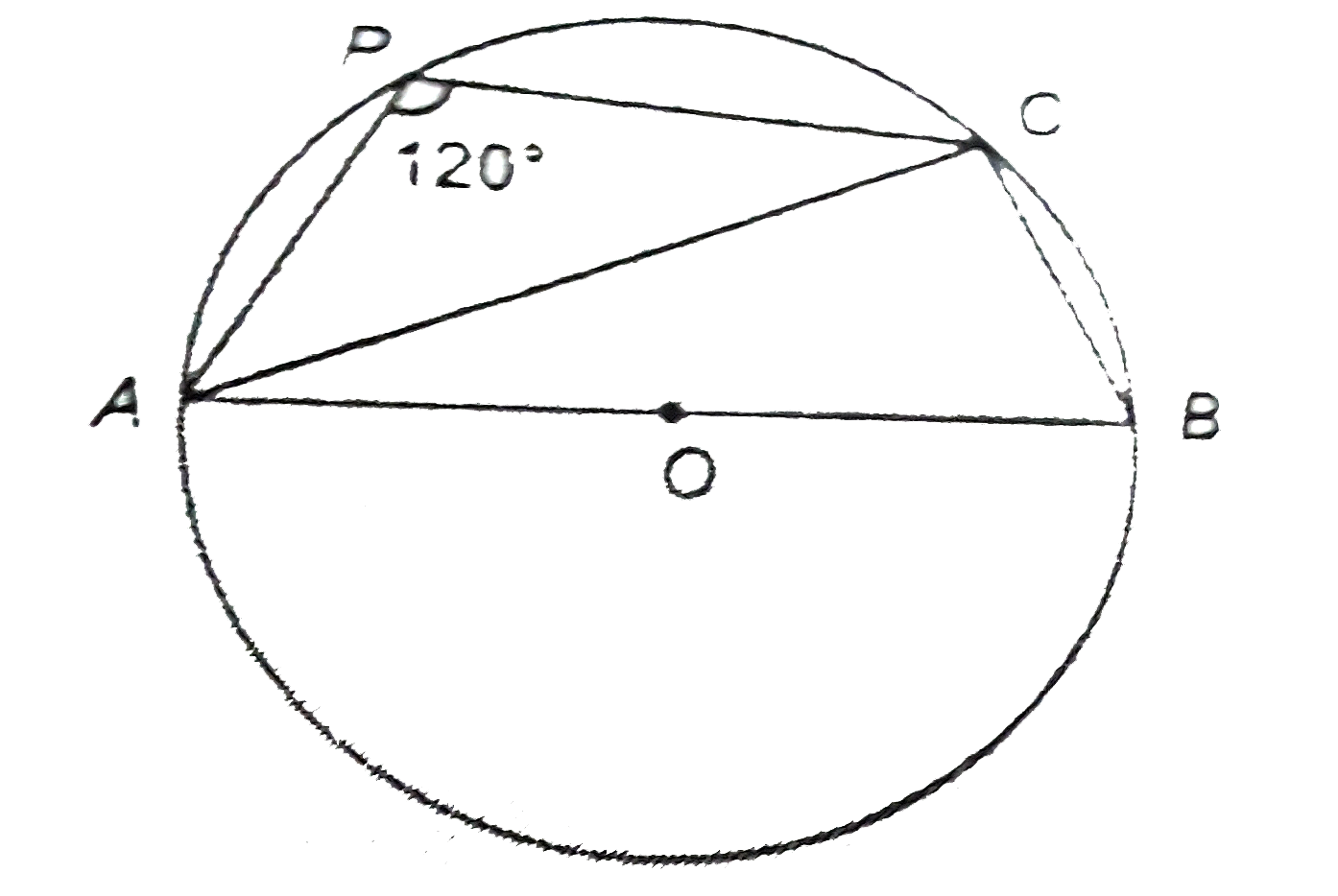 View Solution
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.
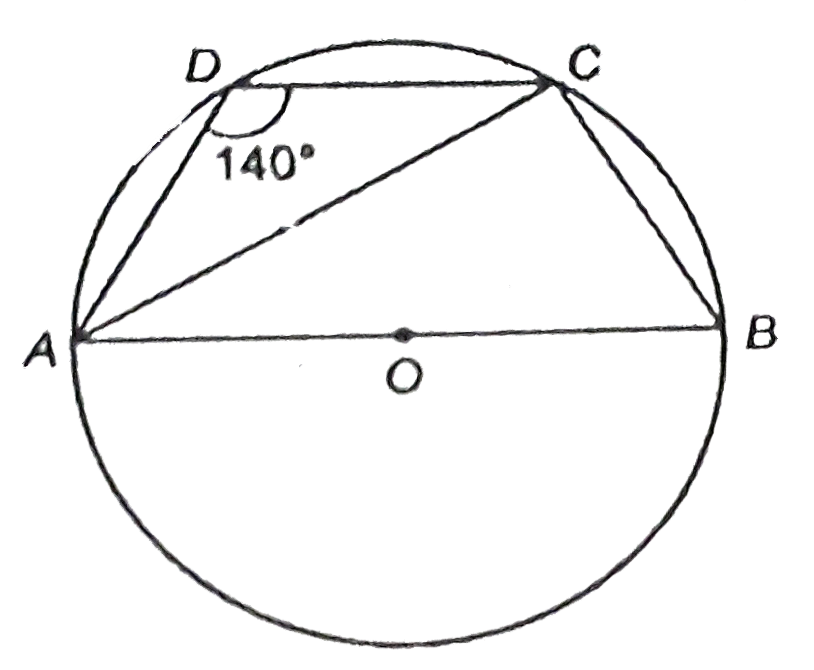 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
PQRS is a cyclic quadrilateral and PQ is the diameter of circle . If ∠RPQ=38∘ , what is the value (in degrees) of ∠PSR ?
A52B77C128D142 - Question 2 - Select One
ABCD is a cyclic trapezium with AB || DC and AB = diameter of the circle. If ∠CAB=30∘, then ∠ADC is
A60∘B120∘C150∘D30∘ - Question 3 - Select One
ABCD is a cyclic quadrilateral such that AB is the diameter of the circle circumscribing it and ∠ADC=145∘ . What is the measure of ∠(BAC) ?
A50∘B35∘C55∘D40∘
In Figure, ABCD is a cyclic quadrilateral. Find the value of x
View SolutionPQRS is a cyclic quadrilateral. PR and QS intersect at T. If ∠SPR=40∘and∠PQS=80∘, then what is the value (in degrees) of ∠PSR?
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=148∘. what is the measure of the ∠BAC ?
ABCD एक चक्रीय चतुर्भुज है, इस प्रकार की AB इसके अंदर वृत्त का व्यास है और ∠ADC=148∘ है। ∠BAC का माप कया हैView SolutionABCD is a cyclic quadrilateral such that AB is the diameter of the circle circumscribing it and ∠ADC=155∘, then what is the measure of ∠BAC?
View SolutionABCD is a cyclic quadrilateral and AD is a diameter. If ∠DAC=55∘ then value of ∠ABC is
View Solution

