In a regiment the ratio between the number of officers to soldiers was 3:31 before battle. In a battle 6 officers and 22 soldiers were killed and the ratio became 1:13, the number of officers in the regiment before battle was:
31
38
21
28
To find the number of officers in the regiment before the battle, we can follow these steps:
Step 1: Set up the initial ratio
The ratio of officers to soldiers is given as 3:31. We can express the number of officers and soldiers in terms of a variable k:
- Number of officers = 3k
- Number of soldiers = 31k
Step 2: Account for the losses in battle
In the battle, 6 officers and 22 soldiers were killed. Therefore, the number of officers and soldiers after the battle will be:
- Officers after battle = 3k−6
- Soldiers after battle = 31k−22
Step 3: Set up the new ratio
After the battle, the ratio of officers to soldiers becomes 1:13. We can express this as:
3k−631k−22=113
Step 4: Cross-multiply to eliminate the fraction
Cross-multiplying gives us:
13(3k−6)=1(31k−22)
Step 5: Expand both sides
Expanding both sides results in:
39k−78=31k−22
Step 6: Rearrange the equation
Now, we will rearrange the equation to isolate k:
39k−31k=78−22
8k=56
Step 7: Solve for k
Dividing both sides by 8 gives:
k=7
Step 8: Find the number of officers before the battle
Now, we can find the number of officers before the battle:
Number of officers=3k=3×7=21
Final Answer
The number of officers in the regiment before the battle was 21.
---
The ratio of officers to soldiers is given as 3:31. We can express the number of officers and soldiers in terms of a variable k:
- Number of officers = 3k
- Number of soldiers = 31k
In the battle, 6 officers and 22 soldiers were killed. Therefore, the number of officers and soldiers after the battle will be:
- Officers after battle = 3k−6
- Soldiers after battle = 31k−22
After the battle, the ratio of officers to soldiers becomes 1:13. We can express this as:
3k−631k−22=113
Cross-multiplying gives us:
13(3k−6)=1(31k−22)
Expanding both sides results in:
39k−78=31k−22
Now, we will rearrange the equation to isolate k:
39k−31k=78−22
8k=56
Dividing both sides by 8 gives:
k=7
Now, we can find the number of officers before the battle:
Number of officers=3k=3×7=21
The number of officers in the regiment before the battle was 21.
Topper's Solved these Questions
Similar Questions
In a regiment the ratio between the number of officers to soldiers was 3:31 before battle . In a battle 6 officers and 22 soldiers were killed and the ratio becomes 1:13 , the number of officers in the regiment before battle was
View Solution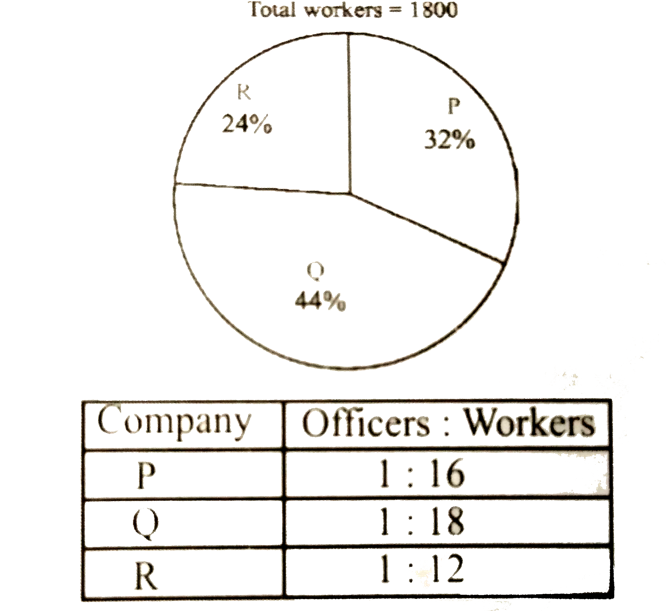
Find the ratio between total number of workers in company P and R together to total number of officers in company P and R together ?
View Solution
Knowledge Check
Before a battle there were the ratio of captains to soldiers was 2 : 7. During the war 25 captains and 100 soldiers were martyred. The new ratio of captains to soldiers became 3 : 10. What is the number of soldiers after the war?
A250B200C150D100What was the respective ratio between the number of soldiers recruited for airforce in the year 2005 and the number of soldiers recruited in army in the year 2009?
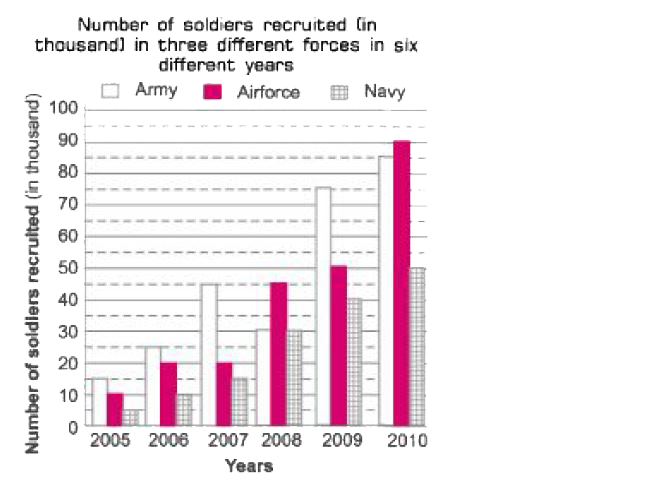 A2:15B5:13C2:17D15:4
A2:15B5:13C2:17D15:4In a school there were 1554 students and the ratio of the number of the boys and girls was 4:3 .After few days, 30 girls joined the school but few boys left , as a result the ratio of the boys and girls became 7:6 .The number of boys who left the school is
A76B74C84D86
Before a battle there were the ratio of captains to soldiers was 2: 7. During the war 25 captains and 100 soldiers were martyred. The new ratio of captions to soldiers became 3 : 10. What is the number of soldiers after the war?
युद्ध से पहले कैप्टन और सिपाहियों का अनुपात 2:7 था। युद्ध के दौरान और 25 कैप्टन और 100 सिपाही शहीद हुए। कैप्टन और सिपाहियों का नया अनुपात 3 : 10 हो गय।॥ युद्ध के बाद सिपाहियों की संख्या क्या होगी?
View SolutionThe ratio between the number of men and women in an office is 5:7. If the number of women working in the office is 56, find the number of men working in the office.
View SolutionThe ratio of the number of students of three class is 2:3:5 .If 20 students are added in each class then the ratio becomes 4:5:7.Find the number of student in each class before adding .
View SolutionIn a school there were 1554 students and the ratio of the number of the boys and girls was 4:3 After few days , 30 girls joined the school but few boys left as a results the ratio of the boys and girls became 7:6 .The number of boys who left the school is .
View SolutionThe ratio of the number of boys to that of girls was 1:2 but when 2 boys and 2 girls left, the ratio became 1:3. How many people were at the party originally ?
View Solution
