is a point on the side AC of and is joined. A line is drawn through a parallel to meeting BC at and another line is drawn through C parallel to meeting AB produced at The
To solve the problem, we will analyze the given geometric configuration step by step.
Step 1: Identify the triangles and parallel lines
We have triangle ABC with point B1 on side AC. The line segment B1B is drawn, and we will draw lines parallel to B1B to form two triangles.
Hint: Look for parallel lines and how they relate to the triangles formed.
Step 2: Draw the parallel lines
1. Draw a line through A1 parallel to B1B that intersects BC.
2. Draw another line through C1 parallel to B1B that intersects the extension of AB.
Hint: Remember that parallel lines create similar triangles.
Step 3: Establish similarity of triangles
From the configuration, we can establish that:
- Triangle AA1C is similar to triangle BB1C because B1B∥A1A.
- Triangle ACC1 is similar to triangle ABB1 because B1B∥C1C.
Hint: Use the properties of similar triangles to set up ratios of corresponding sides.
Step 4: Set up the ratios from the similar triangles
1. From triangle AA1C∼BB1C:
AA1BB1=ACBC
2. From triangle ACC1∼ABB1:
CC1BB1=ACAB
Hint: Write down the ratios clearly to see how they relate to each other.
Step 5: Express one ratio in terms of another
From the first similarity, we can express:
AA1=BB1⋅ACBC
From the second similarity, we can express:
CC1=BB1⋅ACAB
Hint: Substitute these expressions into each other to find a relationship.
Step 6: Combine the equations
Using the expressions from the similar triangles, we can set up the equation:
BB1CC1=ABAC
This implies:
BB1CC1=1−B1CAC
Hint: Look for common terms that can help simplify the equation.
Step 7: Finalize the relationship
By rearranging and substituting, we can derive that:
1CC1=1BB1
This leads us to conclude that:
CC1=BB1
Hint: Check if this conclusion aligns with the properties of the triangles and the parallel lines.
Conclusion
The relationships established through the similar triangles and the parallel lines lead us to the conclusion about the segments CC1 and BB1.
We have triangle ABC with point B1 on side AC. The line segment B1B is drawn, and we will draw lines parallel to B1B to form two triangles.
1. Draw a line through A1 parallel to B1B that intersects BC.
2. Draw another line through C1 parallel to B1B that intersects the extension of AB.
From the configuration, we can establish that:
- Triangle AA1C is similar to triangle BB1C because B1B∥A1A.
- Triangle ACC1 is similar to triangle ABB1 because B1B∥C1C.
1. From triangle AA1C∼BB1C:
AA1BB1=ACBC
2. From triangle ACC1∼ABB1:
CC1BB1=ACAB
From the first similarity, we can express:
AA1=BB1⋅ACBC
From the second similarity, we can express:
CC1=BB1⋅ACAB
Using the expressions from the similar triangles, we can set up the equation:
BB1CC1=ABAC
This implies:
BB1CC1=1−B1CAC
By rearranging and substituting, we can derive that:
1CC1=1BB1
This leads us to conclude that:
CC1=BB1
The relationships established through the similar triangles and the parallel lines lead us to the conclusion about the segments CC1 and BB1.
Topper's Solved these Questions
Similar Questions
P is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQ
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View Solution
Knowledge Check
B1 is a point on the side AC of ΔABC and B1B is joined. A line is drawn through a parallel to B1B meeting BC at A1 and another line is drawn through C parallel to B1B meeting AB produced at C1 The
A1CC1−1AA1=1BB1B1CC1+1AA1=1BB1C1BB1−1AA1=2CC1D1AA1−1CC1=2BB1Thet equatio of the line passing through (a, b) and parallel to the line xa+yb=1 is
Axa+yb=3Bxa+yb=2Cxa+yb=0Dxa+yb+2=0A variable line through (p,q) cuts the axes of co ordinates at A and B respectively. Lines are drawn through A parallel to y-axis and through B parallel to x-axis. If they meet at P, then locus of p is
Axp+yq=1Bpx+qy=1Cxq+yp=1Dqx+py=1
To constuct a triangle similar to a given ΔABC with its sides 73 of the corresponding side of ΔABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect of BC. The points B1,B2,…..,B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C, where C' lines on BC produced. Finally line segment A'C' is drawn parallel to AC.
View SolutionInternal bisector of ∠A of triangle ABC meets side BC at D. A line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F. If a, b, c represent sides of ΔABC, then
View SolutionIf C is a point on the line segement joining A(-3,4) and B(2,1) such that AC = 2BC, then the coordinate of C is
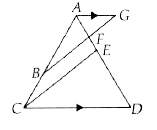
View SolutionIn the given figure (not drawn to scalse ) , AG is parallel to CD and AG=27CD . The point B on AC is such that BC=27AC . If the line BG meets AD at F and the line through C is parallel to BG which meets AD at E , then find the value of FGEC .
View SolutionA straight line through the point (1,1) meets the x-axis at 'A' and the y axis at 'B'. The locus of the mid point of AB is :
View Solution
