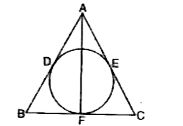
ABC is isosceles triangle where AB = AC which is circumscribed about a circel. If P is the point where the circle touches the side BC, then which of the following is true?

$B P = P C$

$B P > P C$

$B P < P C$

$1 B P = \frac{1}{2} P C$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the properties of the isosceles triangle ABC, where AB = AC, and the circle that is inscribed within it. The point P is where the incircle touches the side BC.
1. Identify the Triangle and Circle:
- We have an isosceles triangle ABC with AB = AC.
- The triangle is circumscribed about a circle (incircle).
2. Label the Points:
- Let the points where the incircle touches the sides be P (on BC), Q (on CA), and R (on AB).
3. Understand Tangent Properties:
- The tangents drawn from a point outside the circle to the circle are equal in length.
- Therefore, if we denote the lengths of the tangents from point A to the points of tangency Q and R as $A P = A Q$ and $A R = A P$ , we can denote:
- $A P = a$
- $B P = b$
- $C P = c$
4. Set Up the Equations:
- Since AB = AC, we have:
- $A P + B P = A B$ (1)
- $A P + C P = A C$ (2)
- From (1) and (2), we can conclude that:
- $a + b = a + c$
5. Simplify the Equations:
- By subtracting $a$ from both sides of the equation $a + b = a + c$ , we get:
- $b = c$
6. Conclusion:
- Since $b = c$ , this means that the lengths from point P to points B and C are equal. Therefore, the segments DP and CP are equal, which confirms that the point P divides BC into two equal segments.
Final Answer:
Thus, we can conclude that $D P = C P$ .

Updated on:7/8/2024