The height of the photosphere is much less than the Sun's radius. Equating gravitational and pressure forces try to estimate the height of the photosphere assuming it to be made up entirely of atomic hydrogen.
The correct Answer is:180 km [Hint . Use the result of Problem 4.7.1]
Since the thickness of the photosphere is small, its density, as well as the acceleration due to gravity, may be assumed constant. for the photosphere to be in a state of equilibrium the hydrostatic pressure must be compensated by the gas pressure, i.e. , where M is the molar mass of the gas. Hence
Similar Questions
We know that the atmospheric pressure on the surface of the earth is because of weight, of the air. The radius of the earth is 6400 km and atmospheric pressure on the sruface of earth is 1×105N/m2. Estimate the mass of the earth's atmosphere assuming that acceleration due to gravity remains constant at 10m/s2 over the entrie height of the atmospehre.
View SolutionA lake filled with water has depth H, A pipe of length slightly less than H lies at the bottom of the lake. It contains an ideal gas filled up to a length of H10 A smooth an ideal gas filled up to a length gas in place. Now the pipe is slowly raised to vertical position (see figure). Assume that temperature of the gas remains Constant and neglect the atmospheric pressure.
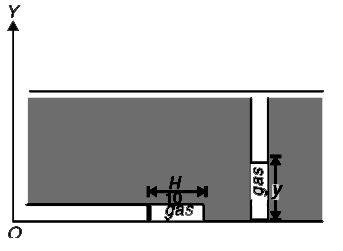
(a) Plot the variation of pressure inside the lake as a function of height y from the base. Let the height of piston frm the base, after the pipe is made vertical, by y. plot the variation of gas pressure as a function of y in the first graph itself.
(b) In equilibrium the gas pressure and the pressure due to water on the piston must be equal. Using this solve for equilibrium height y0 of the piston. You get two answers. Which one is correct and why?
View Solution
Knowledge Check
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
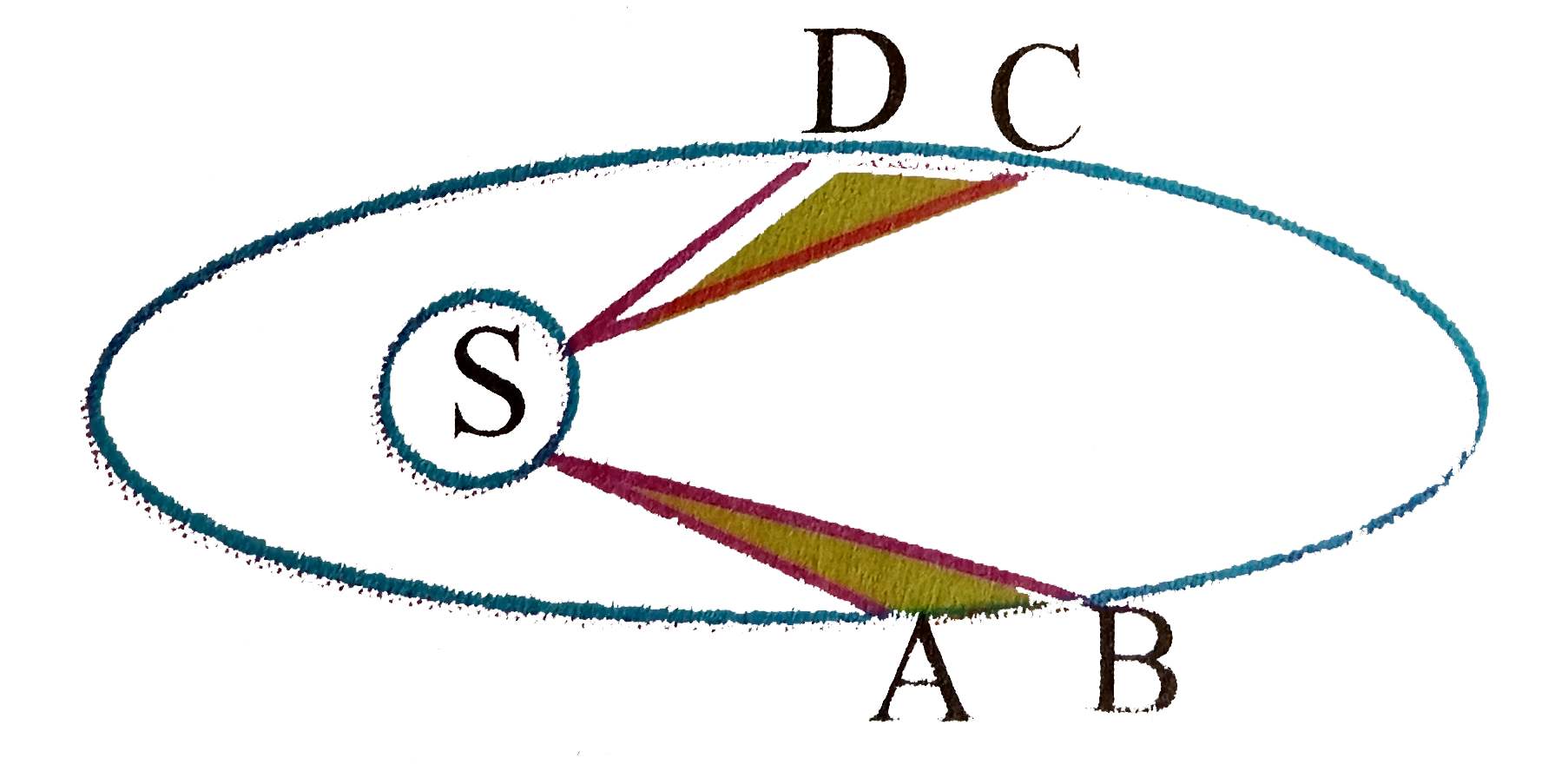 A3GMmaB5GMmaCGMmaDnone of the above
A3GMmaB5GMmaCGMmaDnone of the aboveSuppose the charge of a proton and an electron differ slightly. One of them is -e and the other is (e+Δe). If the net of between force and gravitational force between two hydrogen atoms placed at a distance d (much greater than atomic size) apart is zero, then Δe is of the other [Given mass of hydrogen, mh=1.67×10−27kg]
A10−23CB10−37CC10−47CD10−20CSuppose the charge of a proton and an electron differ slightly. One of them is −e, the other is (e+Δe). If the net of electrostatic force and gravitational force between two hydrogen atoms placed at a distance d (much greater than atomic size) apart is zero. Then Δe is of the order of [Given mass of hydrogen mh=1.67×10−27kg]
A10−23CB10−37CC10−47CD10−20C
Suppose the charge of a proton and an electron differ slightely. One of them is −e, the other is (e+Δe). If the net of electrostatic force and gravitational force between two hydrogen atoms placed at a distance d (much greater than atomic size) apart is zero. Then Δe is of the order of [Given mass of hydrogen mh=1.67×10−27kg]
View SolutionA manometer is connected to a gas containing bulb. The open arm reads 43.7cm whereas the arm connected to the bulb reads 15.6cm. If the barometric pressure is 743mm mercury , calculate the pressure of the gas in bar?
Strategy : The pressure of the gas inside the bulb is greater than the external atmospheric pressure because the height of mercury column in the left arm is less than in the right arm.Therefore ,
pgas(in cm)=patom(in cm)+hcm
View SolutionWater is filled up to a height h in a beaker of radius R as shown in the figure. The density of water is ρ, the surface tension of water is T and the atmospheric pressure is P0. Consider a vertical section ABCD of the water column through a diameter of the beaker. The force on water on one side of this section by water on the other side of this section has magnitude

View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external force
View SolutionThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
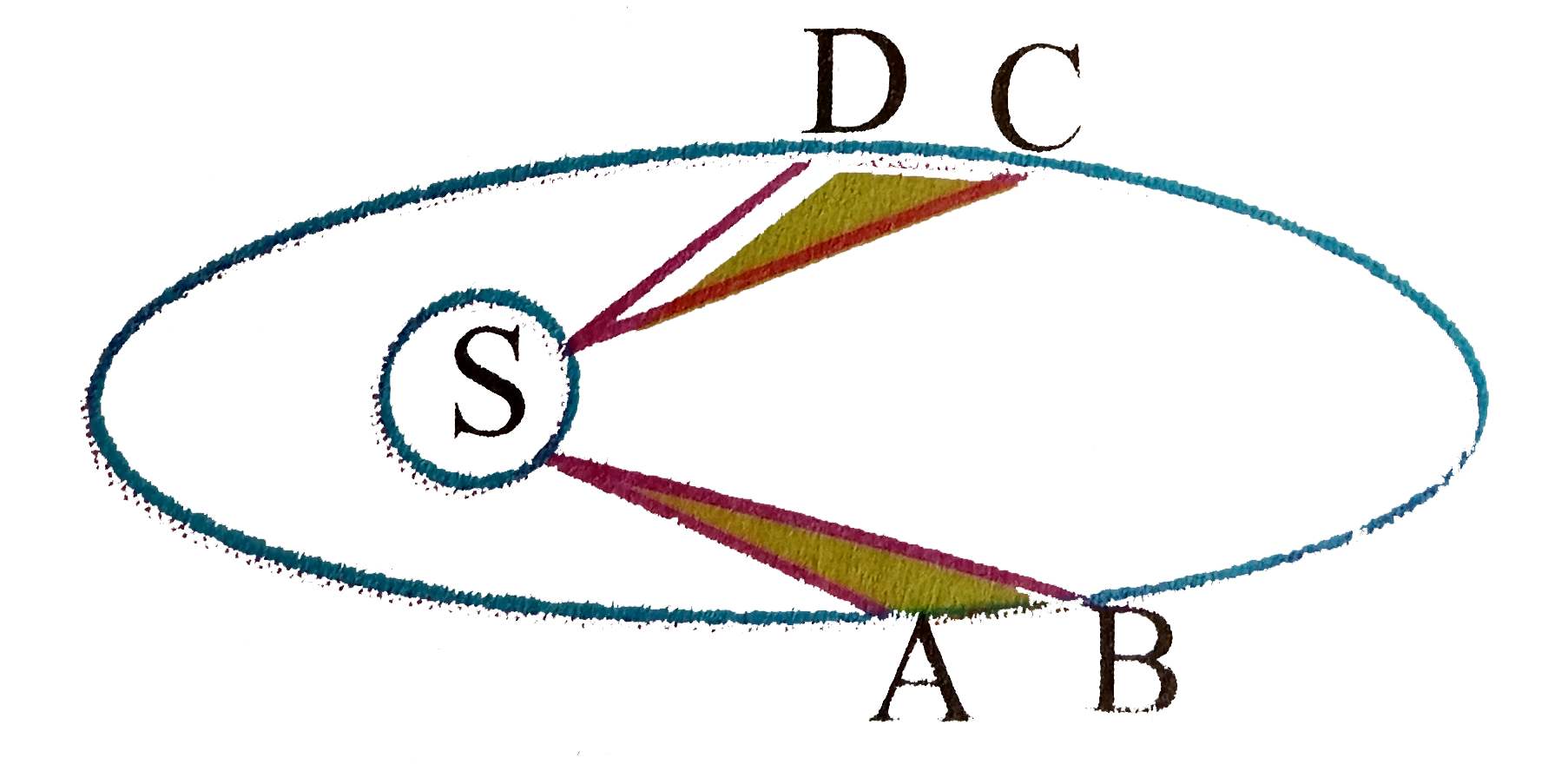
View Solution
