What pressure can a spherical steel container withstand, if its internal radius is R and the wall thickness is d? Do calculations for R = 50 cm, d = 5 mm.
The correct Answer is:2.8×106Pa=28 atm
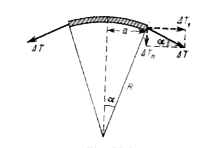
Imagine a small spherical segment with a radius of the base of a=Rsinα to be cut out of the sphere (Fig.). An elementary
elastic force ΔT=σΔS=σdΔl acts on an element of area ΔS=dΔl on the periphery of this segment. The normal component of the elementary force is ΔTn=ΔTsinα=σdΔlα. Summing over the completo circumference of the segment, we obtain the total force of the normal pressure:
Tn=σd.2παsinα=2πσRdsin2α
This force compensates the force of the gaseous pressure F=pS acting on the segment. For a small angle the segment.s area is S=πa2=πR2sin2α, and the force of pressure is F=πpR2sin2α. It follows from the balance of forces that p=2σd/R.
Similar Questions
The maximum surface charge density of a uniformly charged spherical radius R and wall thickness 't', so that it will not burst apart, is
View SolutionWhat internal pressure (in the absence of an external presure) can be sustained
(a) by a glass tube, (b) by a glass spherical flask, if in both cases the wall thickness is equal to Δr=1.0mm and the radius of the tube and the flask equals r=25mm?
View Solution
Knowledge Check
A spherical marble of radius r is made to oscillate in a bowl of radius R. What is its period of oscillation ?
AT=2π√RgBT=2π√R−rgCT=12π√gR−rDT=2π√gRThe maximum surface charge density of a uniformly charged spherical radius R and wall thickness 't', so that it will not burst apart, is
A√σmε0tRB√2σmε0tRC√3σmε0tRD√4σmε0tR
The outer radius of a spherical container is 5 cm and the thickness of the container is 2 cm . Find the volume of the metal content of the shell .
View SolutionThe outer radius of a spherical container is 5 cm and the thickness of the container is 2 cm.Find the volume of the metal content of the shell.
View SolutionThe resistivity of copper is approximately 1.67×10−8Ωm.
Calculate the electrical resistance of a hollow tube made of copper of external radius 20 cm and length 20 cm . The thickness of copper is 50 mm .
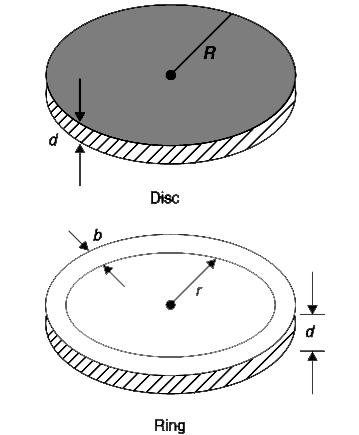
View SolutionA steel ring is to be fitted on a wooden disc of radius R and thickness d. The inner radius of the ring is r which is slightly smaller than R. The outer radius of the ring is r + b and its thickness is d (same as the disc). There is no change in value of b and d after the ring is fitted over the disc, only the inner radius becomes R. If the Young’s modulus of steel is Y, calculate the longitudinal stress developed in it. Also calculate the tension force developed in the ring.
[Take b<<r]
View SolutionA current I flows in a long thin walled cylinder of radius R. What pressure do the walls of the cylinder experience ?
View SolutionA solid sphere of radius 'r' is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm, find the value of 'r' .
View Solution
