The maximum surface charge density of a uniformly charged spherical radius R and wall thickness 't', so that it will not burst apart, is
√σmε0tR
√2σmε0tR
√3σmε0tR
√4σmε0tR
The correct Answer is:D
To find the maximum surface charge density (σ) of a uniformly charged spherical shell with radius R and wall thickness t so that it does not burst apart, we can follow these steps:
Step 1: Understand the Forces Acting on the Shell
When the spherical shell is uniformly charged, each hemisphere experiences an attractive force due to the other hemisphere. This force can lead to stress on the shell.
Step 2: Calculate the Charge on Each Hemisphere
Let Q be the total charge on one hemisphere. The surface charge density σ is defined as the charge per unit area. The area of one hemisphere is given by:
A=2πR2
Thus, the charge Q on one hemisphere can be expressed as:
Q=σ⋅A=σ⋅2πR2
Step 3: Calculate the Force Between Hemispheres
The attractive force F between the two hemispheres can be calculated using Coulomb's law:
F=kQ2r2
where k is the Coulomb's constant and r is the distance between the centers of mass of the two hemispheres, which is equal to R.
Substituting Q into the force equation:
F=k(σ⋅2πR2)2R2=k4π2σ2R4R2=4π2kσ2R2
Step 4: Relate the Force to Maximum Stress
The maximum stress σm that the material can withstand before bursting is given by:
Stress=ForceArea
The area on which this force acts is the area of the shell, which can be approximated as:
A=2πR⋅t
Thus, the stress can be expressed as:
σm=FA=4π2kσ2R22πRt=2πkσ2Rt
Step 5: Solve for Maximum Surface Charge Density
Rearranging the equation to solve for σ:
σ2=σmt2πkR
Taking the square root gives:
σ=√σmt2πkR
Step 6: Substitute k with 14πϵ0
Substituting k into the equation:
σ=
⎷σmt2π⋅14πϵ0R=√4π2σmϵ0t2R=√2σmϵ0tR
Final Result
Thus, the maximum surface charge density is given by:
σ=√2σmϵ0tR
When the spherical shell is uniformly charged, each hemisphere experiences an attractive force due to the other hemisphere. This force can lead to stress on the shell.
Let Q be the total charge on one hemisphere. The surface charge density σ is defined as the charge per unit area. The area of one hemisphere is given by:
A=2πR2
Thus, the charge Q on one hemisphere can be expressed as:
Q=σ⋅A=σ⋅2πR2
The attractive force F between the two hemispheres can be calculated using Coulomb's law:
F=kQ2r2
where k is the Coulomb's constant and r is the distance between the centers of mass of the two hemispheres, which is equal to R.
F=k(σ⋅2πR2)2R2=k4π2σ2R4R2=4π2kσ2R2
The maximum stress σm that the material can withstand before bursting is given by:
Stress=ForceArea
The area on which this force acts is the area of the shell, which can be approximated as:
A=2πR⋅t
Thus, the stress can be expressed as:
σm=FA=4π2kσ2R22πRt=2πkσ2Rt
Rearranging the equation to solve for σ:
σ2=σmt2πkR
Taking the square root gives:
σ=√σmt2πkR
Substituting k into the equation:
σ=
⎷σmt2π⋅14πϵ0R=√4π2σmϵ0t2R=√2σmϵ0tR
Thus, the maximum surface charge density is given by:
σ=√2σmϵ0tR
Similar Questions
Knowledge Check
A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of these
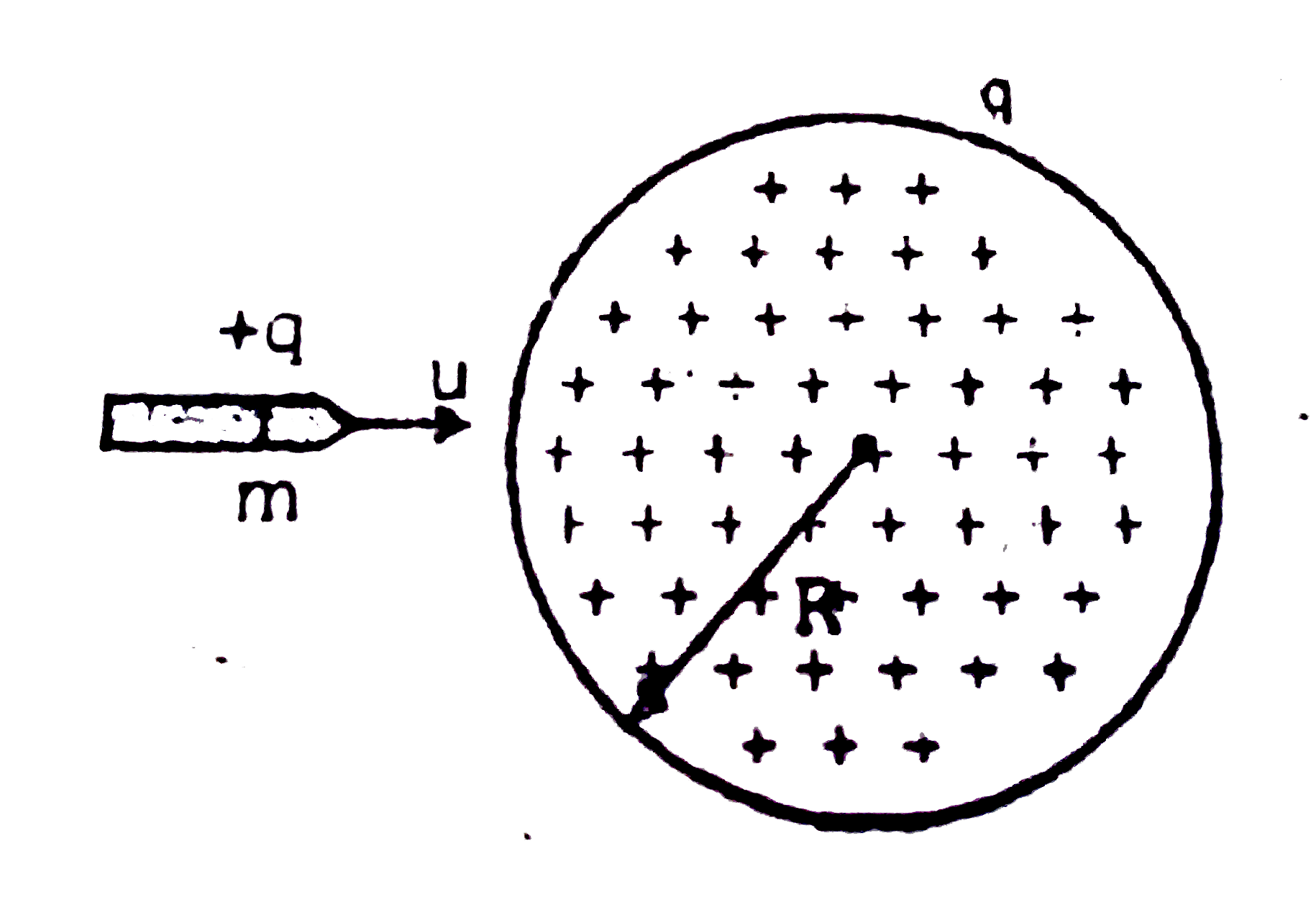
A bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surface of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surface is .

View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionAn annular disc of inner radius a and outer radius '2a' is uniformly charged with uniform surface charge density σ. Find the potential at a distance 'a' from the centre at a point 'P' lying on the axis.
View SolutionThe electric potential due to uniformly charged sphere of radius R,having volume charge density rho having a spherical cavity of radius R2 as shown as in figure at point p is
_PHY_E05_288_Q01.png)
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View Solution
