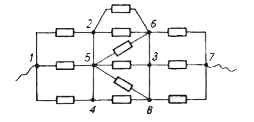
A cube is soldered together írom identical pieces of wire each of a resistance r. It is connected to the circuit at the corners lying on opposite ends of a body diagonal Find the equivalent resistance.

The correct Answer is:R=r3+r6+r3=5r5
It is clear from considerations of symmetry that the potentials at points 2, 4 and 5 coincide, i.e. Ψ2=Ψ4=Ψ6=Ψ Hence the potentials at points δ,δand3 coincide as well: Ψ5=Ψ5=Ψ3=Ψ... If we short circuit the points at equal potential, i.e. connect the points by means of conductors of negligible resistance, the resistance of the circuit remains unchanged. The circuit obtained in this way is shown in Fig. 26.51. Its resistance is equal to tho sum of the resistances of three series connected sections of three, six, and three parallel connected branches each.
Similar Questions
A regular hexagon is formed by six wires each of resistance rΩ and the corners are joined to the center by wires of the same resistance. If the current enters at one corner and leaves at the opposite corner, find the equivalent resistance of the conductor.
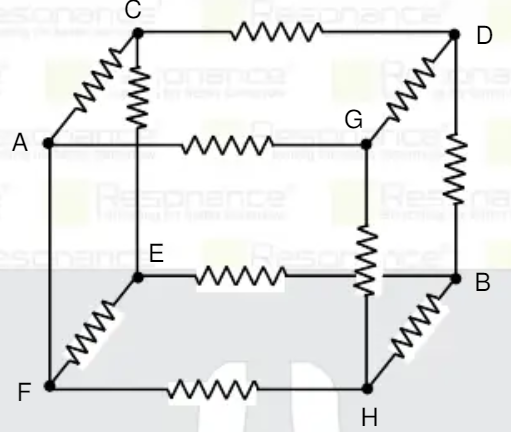
View SolutionA cube made up of wire each of resistance R. The find equivalent resistance across its diagnol
View Solution
Knowledge Check
Twelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
A6ΩB12ΩC5ΩD10ΩTwelve equal wires each of resistance rΩ form a cube. The effective resistance between the corners of the same edge of the cube is
A712rB127rC57rD125rTwelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
A56Ω and 12AB65Ω and 12 AC56Ω 4AD65Ω and 4A
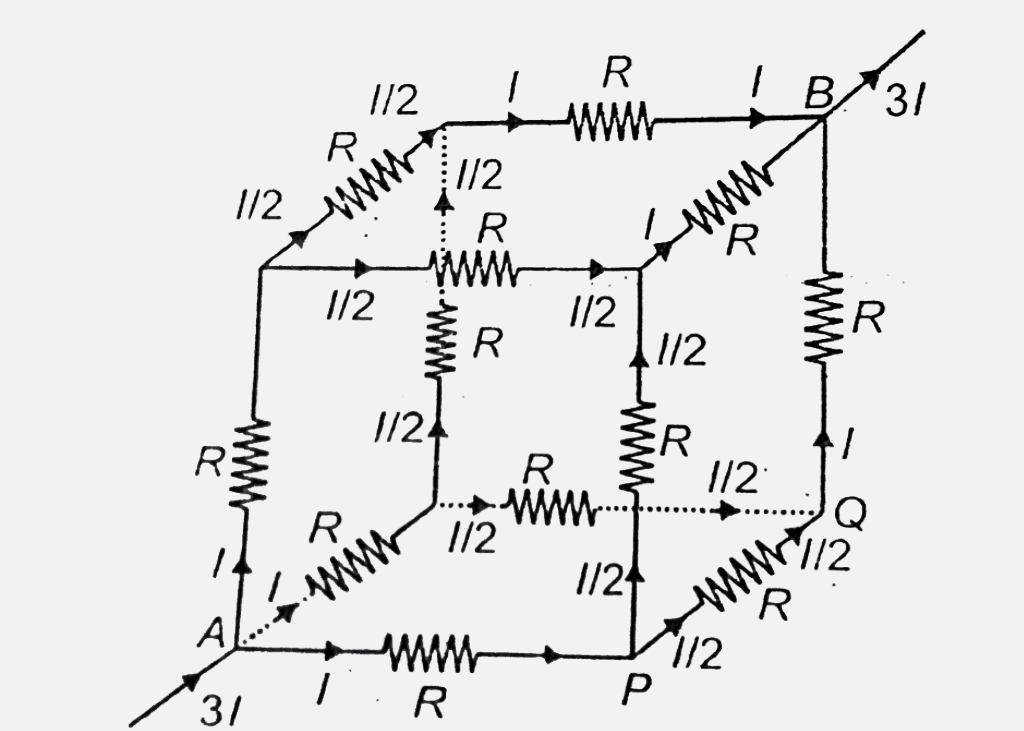
Tweve identical resistance each of resistance R are joined to form a cube as shown in figure.
Find resistance of the combination across AB
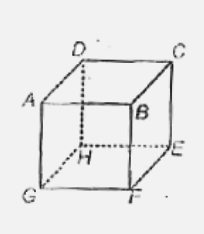
View SolutionTwelve wires of equal resistacne R are connected to form a cube . The effective resistance between two diagonal ends A and E will be .
View SolutionEleven equal wires each of resistance r form the edges of a incomplete cube. Find the total resistance from one end of the vacant edge of the cube to the other.
View SolutionA piece of wire having a resistance ‘R’ is cut into six equal parts. These are then connected in parallel to get an equivalent resistance of ‘R^1’. The ratio of R1R is:
View SolutionFour wires each of same length diameter and material are connected to each other to form a square. If the resistance of each wire is R then equivalent resistance across the opposite corners is
View Solution
