An electron accelerated in an electric field of 20 kV enters a uniform magnetic field with induction 0.1 T. Its velocity vector makes an angle of 75∘ with the magnetic field vector. Find the shape of the path.
The correct Answer is:A helix winding around the lines of induction. The radius of the circle is 23mm, the bitch is 39mm.
In the field the electron acquires a kinetic energy of 20 kev, which is much less than its rest energy (511 kcV). Therefore in this problem it is a nonrelativistic particle. Resolve the electron velocity into two comportents: one along the line of induction, and the other perpendicular to it, v⊥=vsina (Fig. 28.5). No forces act on the electron in the longitudinal direction, therefore the electron will move at a constant speed along the z-axis according to the equation. z0+vtcosα
In the lateral direction (i.e. in the my plane) the electron is acted upon by the Lorentz force, which makes the projection of its motion in this plane a circle with radius R=mv⊥eB=√2meΨsinαeB
and with period T2πm/eB In space the election moves along a helix which winds around the lines of induction. The radius of the circle, R, was given above. The pitch of the helix is h=v1T2πmvcosαeB−2πRcotα. 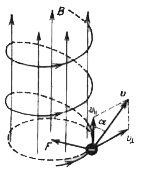
Similar Questions
A beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helical path taken by the proton beam.
View SolutionA beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helicla path taken by the proton beam and the pitch of the helix.
View Solution
Knowledge Check
A charged particle enters into a magnetic field with velocity vector making an angle of 30∘ with respect of the direction of magnetic field. The path of the particle is
AcircularBhelicalCellipticalDstraight lineA charged enters a unifrom magnetic field with velocity vector at an angle of 45∘ with the magnetic field . The pitch of the helical path followed by the particles is ρ . The radius of the helix will be
Ap√2πB√2PCp2πD√2pπAn electron having momentum 2.4×10−23 kg m s−1 enters a region of uniform magnetic field of 0.15 T. The field vector makes an angle of 30∘ with the initial velocity vector of the electron. The radius of the helical path of the electron in the field shall be
A2mmB1mmC√32 mmD0.5mm
A beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helicla path taken by the proton beam and the pitch of the helix.
View SolutionA beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helicla path taken by the proton beam and the pitch of the helix.
View SolutionA beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helicla path taken by the proton beam and the pitch of the helix.
View SolutionAn electron having momentum 2.4×10−23 kg m s−1 enters a region of uniform magnetic field of 0.15 T. The field vector makes an angle of 30∘ with the initial velocity vector of the electron. The radius of the helical path of the electron in the field shall be
View SolutionA charged particle enters a uniform magnetic field with velocity vector at angle of 45∘ with the magnetic field. The pitch of the helical path followed by the particle is p. the radius of the helix will be
View Solution
