Table 29.10 gives the coordinates of some of the points of the asymptotic hysteresis cycle of a ferromagnetic material. Plot the hysteresis loop. (The recommended scale is 10 mm = 100 A/m and 10 mm 0.20 T.) Find the coercive  force and saturation induction from the graph. Calculate the saturation magnetization and remnant magnetization Mr.
force and saturation induction from the graph. Calculate the saturation magnetization and remnant magnetization Mr.
The correct Answer is:μmax=9.6×103 at H=75 A/m.
The right-hand half of the hysteeresis loop is plotted using the data given in the table, the left-hand half is plotted sysmmetrically  (Fig 29.10). The coercive froe is determined at the point of intersection of the graph wth the H-axis, saturation induction is the point where the upper and lower branches of the loop interest. The saturation magnetization is Msat=Bsatμ0−Hsat≈Bsatμ0 for Bsat>>μ0Hsat. The residual magnetiztion is Mr=Br/μ0, where Br is determined at the point of intersection of the graph with the B-axis.
(Fig 29.10). The coercive froe is determined at the point of intersection of the graph wth the H-axis, saturation induction is the point where the upper and lower branches of the loop interest. The saturation magnetization is Msat=Bsatμ0−Hsat≈Bsatμ0 for Bsat>>μ0Hsat. The residual magnetiztion is Mr=Br/μ0, where Br is determined at the point of intersection of the graph with the B-axis.
Similar Questions
The core and the armature of an electromagnet with dimensions in millimeters as shown in Fig. 30.16 have been manufactured from a ferromagnetic material whose properties have been described in Problem 29.10. What is the force with which the core attracts the armature, if the material has been magnetized to saturation? What force will remain active after the current is switched off?
View SolutionThe absolute magnetic permeability μ of a specimen of magnetic material is related to magnetic intensity H according to the relation as μ=0.6H+8.0×10−4TAm−1. Find the value of H (in Am−1) for which magnetic induction of 0.22T can be produced.
View SolutionThe magnetic scalar potential due to a magnetic dipole at a point on its axis situated at a distance of 20cm from its centre is found to be 1.2×10−5Tm. Find the magnetic moment of the dipole.
View SolutionThe magnetic scalar potential due to a magnetic dipole at a point on its axis situated at a distance of 20cm from its centre is found to be 1.2×10−5Tm. Find the magnetic moment of the dipole.
View SolutionA bar magnet is 0.10 m long and its pole strength is 120 Am . Find magnitude of magnetic field at a point on its axis at a distance 20 cm from it .
View SolutionA bar magnet is 0.10 m long and its pole strength is 120 Am . Find magnitude of magnetic field at a point on its axis at a distance 20 cm from it .
View SolutionA charged particle moves along a circle of radius r=100mm in a unifrom magnetic field with induction B=10.0mT. Find its velocity and perios of revolution if that particle is
(a) a non-relativistic proton,
(b) a relativistic electron.
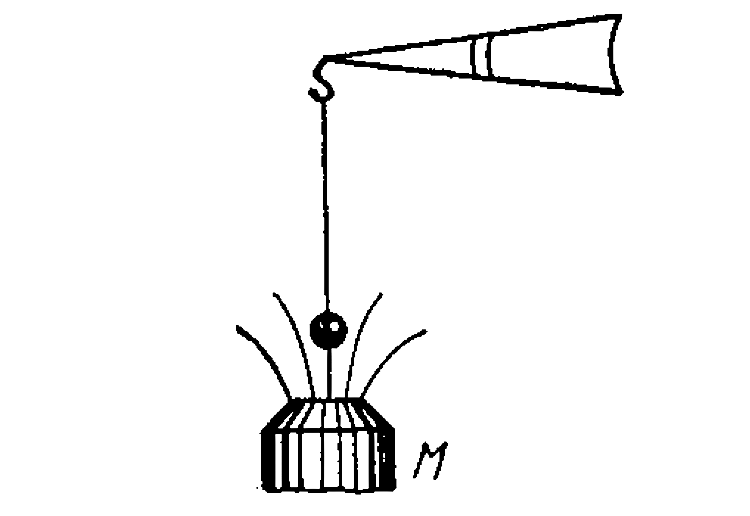
View SolutionIn the arrangement shown in Fig it is possible to measure (by means of a balance) the force with which a paramagnetic ball of volume V=41mm3 is attrated to a pole of the electromagnet M. The magnetic induction at the axis of the poleshoe depends on the height x as B=B0 exp (−ax2), where B0=1.50T,a=100m−2. Find:
(a) at what height xm the ball experiences the maximum attraction,
(b) the magnetic suspeptibility of the paranagnetic if the maximum attraction force equals Fmax=160μN.
View SolutionA magnet of length 0.2 m balances the earth's horizontal field at a point 0.2 m from the nearer pole. The magnet is placed with its north pole pointing south. Find its magnetic moment. [Horizontal induction of earth's field =3.6×10−5 tesla]
View Solutiona) A circular loop of Radius R carries a current I. Obtain an expression for the magnetic field at a point on its axis at a distance of x from its centre. b) A conducting rod of length 2 m is placed on a horizontal table in north-south direction. It carries a current of 5 A from south to north. Find the direction and magnitude of magnetic force acting on the rod. Given that Earth's magnetic field at the place is 0.6×10−4T and angle of dip is (π6)
View Solution
