What time does it take for the current in a circuit made up of a coil and a resistor to reach 0.9 of its stationary value?
The correct Answer is:t=2.3L/R
According to the result of the previous problem we have for i=0.91M an exponential equation 0.9IM an exponential equationi 0.9IM=IM(1−e−t/π),ore−t/τ=0.1
Taking the logarithms, we obtain −tτloge=log0,1,−tτ0.434=−1
Hence t=2.3τ.
Similar Questions
When you have learned to integrate, try to analyze the process of shorting a circuit made up of a coil and a resistor connected to a power supply with constant e.m.f., i.e. the dependence of the current on time. Assume the coil to be without a ferromagnetic core.
View SolutionWhen you have learned to integrate, try to analyze the process of shorting a circuit made up of a coil and a resistor connected to a power supply with constant e.m.f., i.e. the dependence of the current on time. Assume the coil to be without a ferromagnetic core.
View Solution
Knowledge Check
A circuit consists of a coil, a switch and a battery, all in series. The interval resistance of the battery is negligible compared with that of the coil. The switch is originally open. It is thrown closed, after a time interval Δt. The current in the circuit reaches 80.0% of its final value. The switch then remains closed for a time interval much longer than Δt. The wires connected to the terminals of the battery are then short circuited with another wire and removed from the battery, so that the current is uninterrupted.
At the moment 2Δt after the coil is short-circuited, the current in the coil is what percentage of its maximum value?A20.0%B8.0%C4.0%D10.0%A circuit consists of a coil, a switch and a battery, all in series. The interval resistance of the battery is negligible compared with that of the coil. The switch is originally open. It is thrown closed, after a time interval Δt. The current in the circuit reaches 80.0% of its final value. The switch then remains closed for a time interval much longer than Δt. The wires connected to the terminals of the battery are then short circuited with another wire and removed from the battery, so that the current is uninterrupted.
At an instant that is a time interval Δt. After the short circuit, the current is what percentage of its maximum value?A20.0%B8.0%C4.0%D10.0%
A solenoid having an inductance of 9.70 μH is connected in series with a 1.20 kΩ resistor. (a) If a 14.0 V battery is connected across the pair, how long will it take for the current through the resistor to reach 40.0% of its final value? (b) What is the current through the resistor at time t=0.50τL?
View SolutionExpress the inductance of a serise connected circuit made up of a resistor, a coil and a capacitor in terms of its Q-factor and the frequency ratio γ=ω/ω0 .
View SolutionA circuit consists of a coil, a switch and a battery, all in series. The internal resistance of the battery is negligible compared with that of the coil. The switch is originally open. It is thrown closed, after a time interval Δt. The current in the circuit reaches 80.0% of its final value. The switch then remains closed for a time interval much longer than Δt. The wires connected to the terminals of the battery are then short circuited with another wire and removed from the battery, so that the current is uninterrupted.
At an instant that is a time interval Δt. After the short circuit, the current is what percentage of its maximum value? a)20% b) 8% c) 4% d)10 %
View SolutionThe current in a LR circuit builds up to 34th of its steady state value in 4s. The time constant of this circuit is
View SolutionA potential difference of 4V is applied to a coil of resistance 8Ω and inductance 8H. How long does it take for the current to reach half of its final value ?
View Solution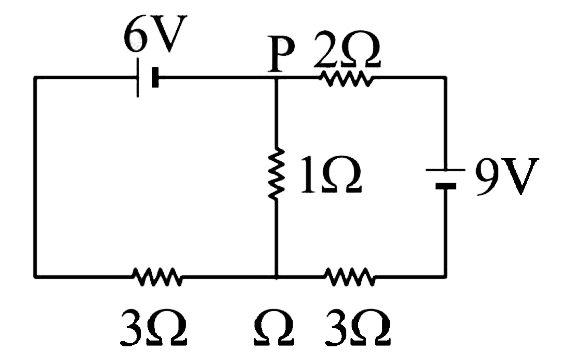
In the circuit shown, what is the current (in A) in the 1Ω resistor?
View Solution
