A circuit consists of a coil, a switch and a battery, all in series. The internal resistance of the battery is negligible compared with that of the coil. The switch is originally open. It is thrown closed, after a time interval Δt. The current in the circuit reaches 80.0% of its final value. The switch then remains closed for a time interval much longer than Δt. The wires connected to the terminals of the battery are then short circuited with another wire and removed from the battery, so that the current is uninterrupted.
At an instant that is a time interval Δt. After the short circuit, the current is what percentage of its maximum value?
a)20% b) 8% c) 4% d)10 %
20.0%
8.0%
4.0%
10.0%
The correct Answer is:A
To solve the problem step by step, we will analyze the circuit behavior before and after the switch is short-circuited.
Step 1: Understanding the Circuit
The circuit consists of a coil (inductor), a switch, and a battery in series. The internal resistance of the battery is negligible compared to the resistance of the coil.
Step 2: Current Growth in the Inductor
When the switch is closed, the current in the inductor grows according to the formula:
I(t)=ER(1−e−LtR)
where:
- E is the EMF of the battery,
- R is the resistance of the coil,
- L is the inductance of the coil,
- t is the time after the switch is closed.
Step 3: Current After Time Interval Δt
After a time interval Δt, the problem states that the current reaches 80% of its maximum value:
I(Δt)=0.8Imax
where Imax=ER.
Substituting this into the current equation:
0.8ER=ER(1−e−LΔtR)
Step 4: Simplifying the Equation
Dividing both sides by ER:
0.8=1−e−LΔtR
Rearranging gives:
e−LΔtR=1−0.8=0.2
Step 5: Finding Δt
Taking the natural logarithm of both sides:
−LΔtR=ln(0.2)
Thus:
Δt=−RLln(0.2)
Step 6: Current After Short Circuit
After the switch is closed for a long time, the current reaches its maximum value Imax. When the battery is short-circuited, the current starts to decay according to the formula:
I(t)=Imaxe−RtL
Step 7: Current After Time Interval Δt Post Short Circuit
We need to find the current I at a time interval Δt after the short circuit:
I(Δt)=Imaxe−RΔtL
Substituting Δt=−RLln(0.2):
I(Δt)=Imaxe−RL⋅−RLln(0.2)
This simplifies to:
I(Δt)=Imaxeln(0.2)
I(Δt)=Imax⋅0.2
Step 8: Finding the Percentage of Maximum Current
Thus, the current I at time Δt after the short circuit is:
I=0.2Imax
This means the current is 20% of its maximum value.
Final Answer
The correct answer is:
a) 20%
The circuit consists of a coil (inductor), a switch, and a battery in series. The internal resistance of the battery is negligible compared to the resistance of the coil.
When the switch is closed, the current in the inductor grows according to the formula:
I(t)=ER(1−e−LtR)
where:
- E is the EMF of the battery,
- R is the resistance of the coil,
- L is the inductance of the coil,
- t is the time after the switch is closed.
After a time interval Δt, the problem states that the current reaches 80% of its maximum value:
I(Δt)=0.8Imax
where Imax=ER.
0.8ER=ER(1−e−LΔtR)
Dividing both sides by ER:
0.8=1−e−LΔtR
Rearranging gives:
e−LΔtR=1−0.8=0.2
Taking the natural logarithm of both sides:
−LΔtR=ln(0.2)
Thus:
Δt=−RLln(0.2)
After the switch is closed for a long time, the current reaches its maximum value Imax. When the battery is short-circuited, the current starts to decay according to the formula:
I(t)=Imaxe−RtL
We need to find the current I at a time interval Δt after the short circuit:
I(Δt)=Imaxe−RΔtL
I(Δt)=Imaxe−RL⋅−RLln(0.2)
This simplifies to:
I(Δt)=Imaxeln(0.2)
I(Δt)=Imax⋅0.2
Thus, the current I at time Δt after the short circuit is:
I=0.2Imax
This means the current is 20% of its maximum value.
The correct answer is:
a) 20%
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Multiple Correct Answer
3 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Switch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View Solution
In given LR circuit the switch S is closed at time t=0 then
View SolutionDetermine the current through the battery in the circuit shown in figure.
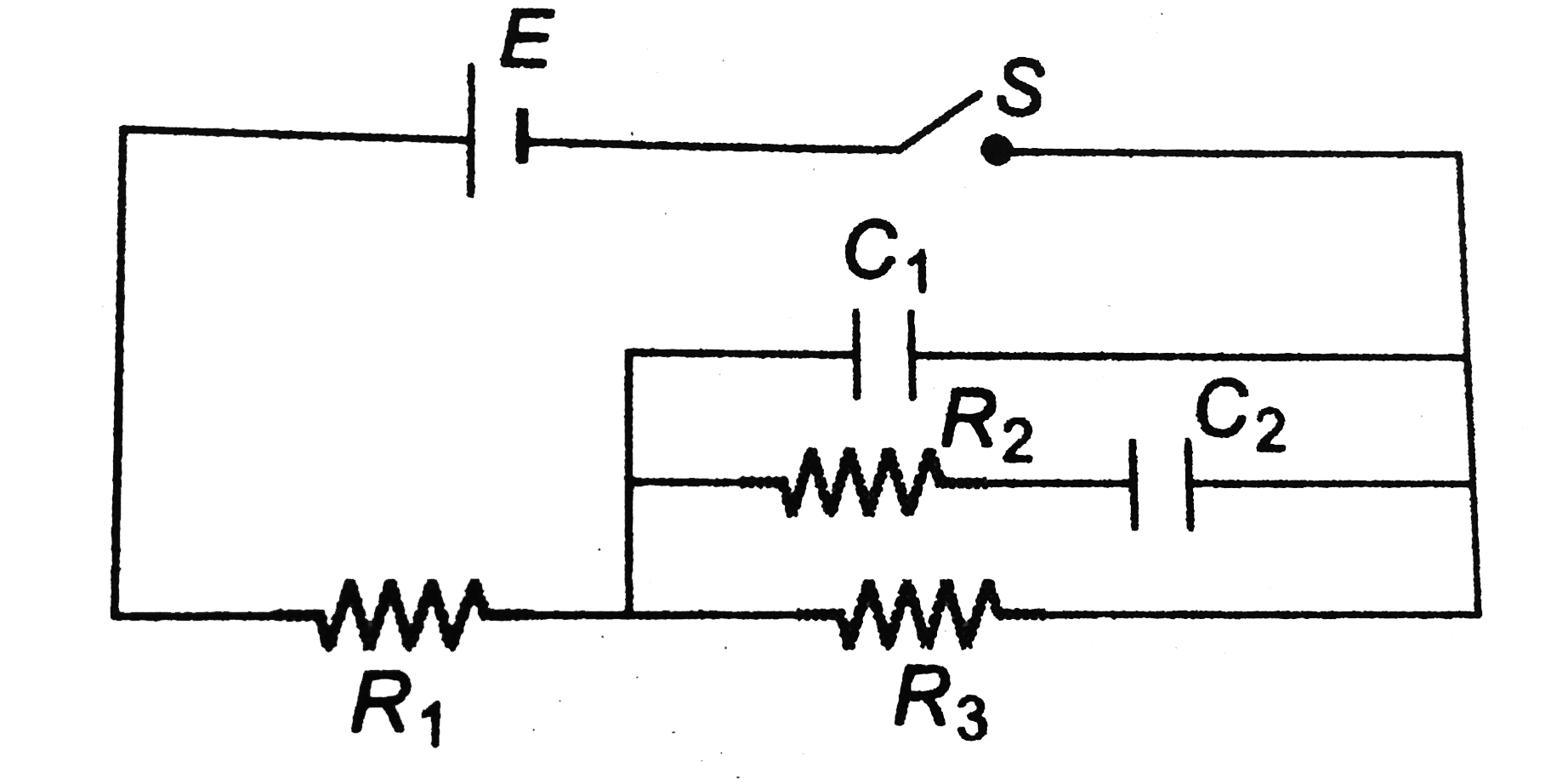
(a) immediately after the switch S is closed
(b) after a long time.
View SolutionPassage-III
In the circuit shown, the battery is ideal with emf V. The capacitor is initially uncharged. The switch is closed at time t = 0
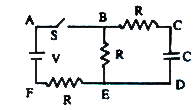
The current in the branch BE at t=∞ is
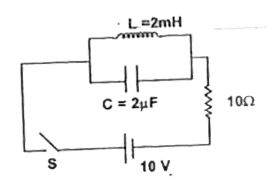
View SolutionThe switch S is closed in the circuit shown at time t=0 . The current in the resistor at t=0 and t=∞ are respectively .
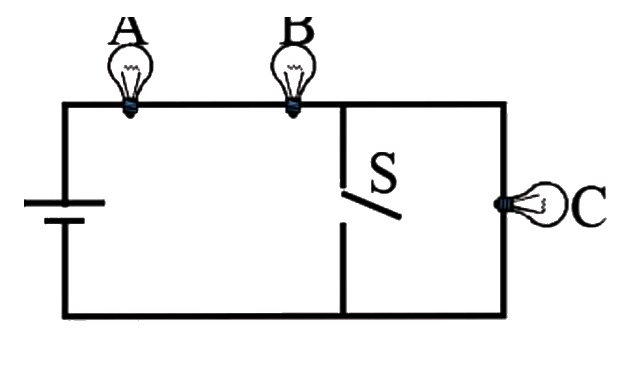
View SolutionA circuit consists of three identical lamps connected to a battery as shown in the figure. When the switch S is closed then the intensities of lamps A and B
View SolutionThe ratio of initial to final current through the battery when the switch is closed in the figure is
View SolutionIn the circuit diagram the current through the battery immediately after the switch S is closed is
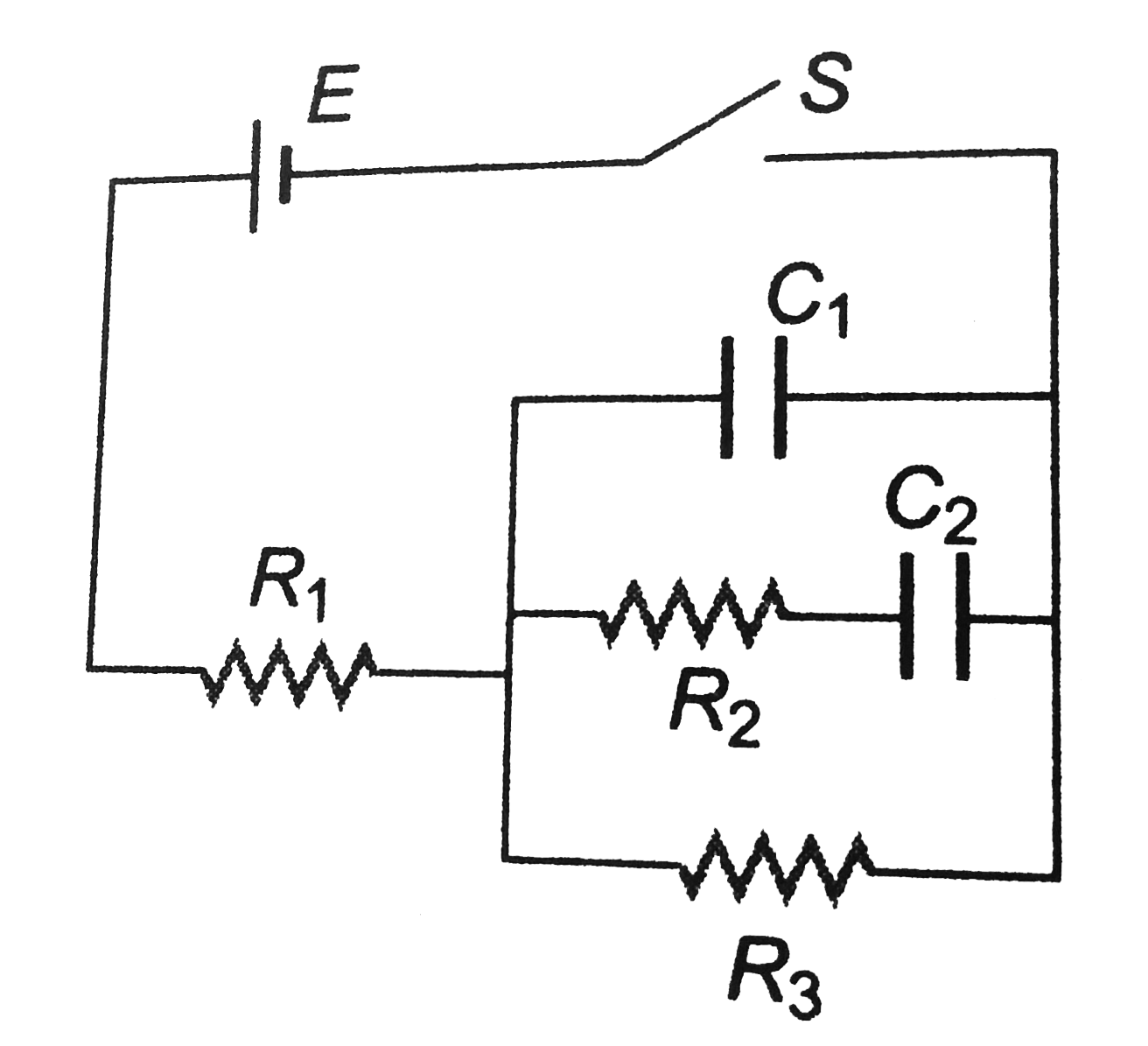
View SolutionIn the circuit shown in figure switch S is closed at time t=0

Current I from the battery at time t is given by
View SolutionIn the circuit shown in figure the switch S is closed at t = 0. A long time after closing the switch
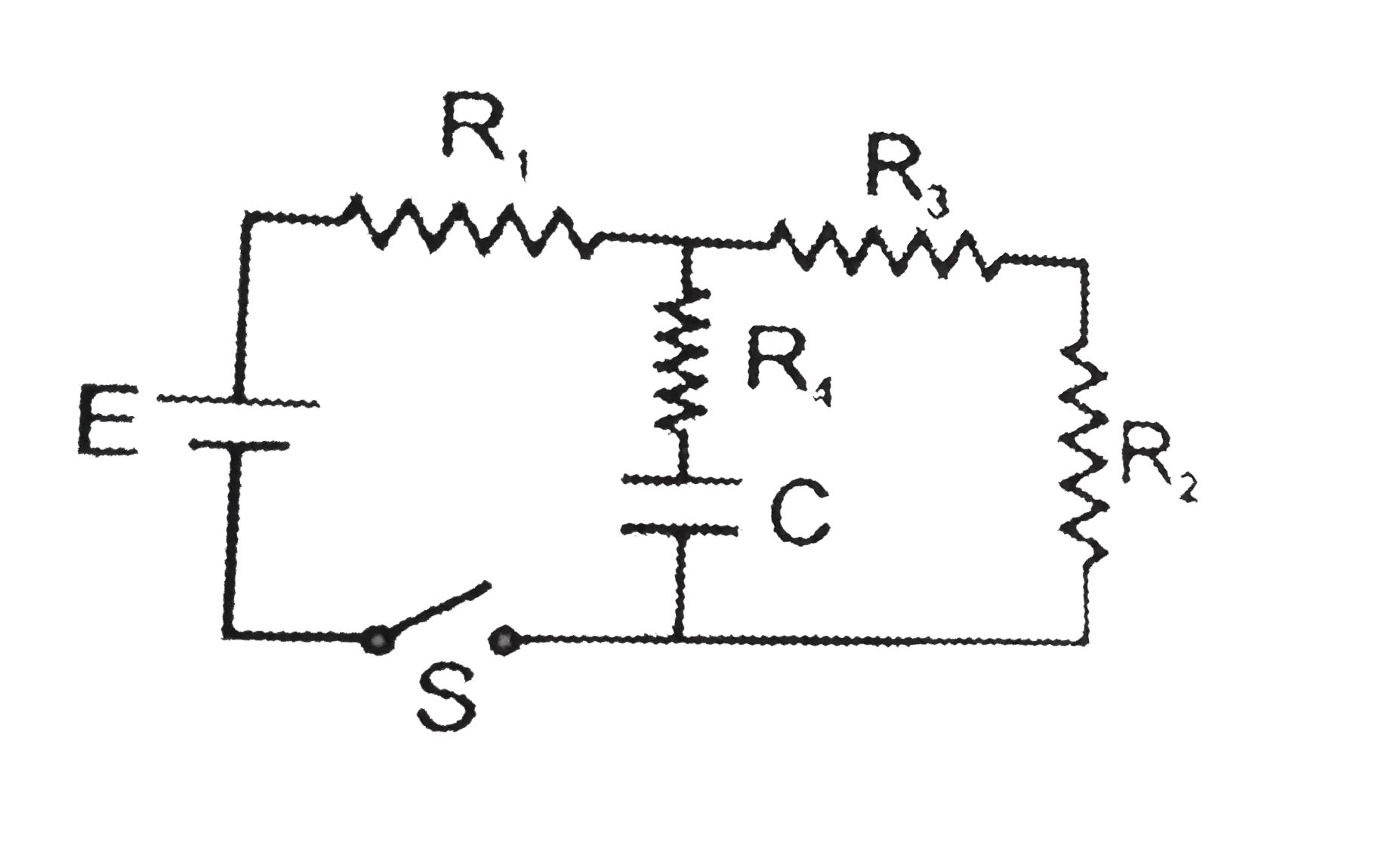
View Solution
